LIngkaran

Lingkaran

Lingkaran adalah tempat kedudukan titik-titik yang jaraknya sama dari suatu titik tertentu (disebut pusat lingkaran).

Jarak yang sama itu disebut jari-jari.

Ruas garis yang menghubungkan pusat lingkaran dengan salah satu titik pada lingkaran juga disebut jari-jari.

Daerah yang dibatasi oleh lingkaran disebut daerah lingkaran.

A. Lingkaran dan busur lingkaran

Bagian dari lingkaran disebut busur lingkaran

Busur yang lebih kecil disebut busur minor (pada gambar berwarna biru) dan bagian yang lebih besar disebut busur mayor (berwarna merah).

Jika hanya disebutkan kata busur, maka yang dimaksud adalah busur minor.

Besarnya ­ BC ditentukan oleh besarnya ∠BAC = α (Titik A adalah pusat lingkaran)

Dalam matematika,

- Sudut α disebut sudut pusat yang menghadap pada ­BC.

Sudut pusat adalah sudut yang titik sudutnya terletak pada pusat lingkaran dan kaki-kaki sudutnya adalah jari-jari lingkaran

Sudut θ disebut sudut keliling yang menghadap pada BC

Sudut keliling adalah sudut yang titik sudutnya terletak pada lingkaran dan kaki-kaki sudutnya berupa tali busur.

Tali busur adalah ruas garis yang menghubungkan dua titik pada lingkaran.

Sifat-sifat sudut pada lingkaran:

1. Sudut keliling yang menghadap pada busur yang sama, besarnya sama.

2. Sudut pusat besarnya dua kali sudut keliling yang menghadap pada busur yang sama.

3. Sudut keliling yang menghadap pada diameter lingkaran, adalah sudut siku-siku.

B. Lingkaran dan garis lingkaran

1. Garis singgung berpotongan dengan lingkaran di satu titik.

2. Titik potong lingkaran dengan garis singgung disebut titik singgung.

3. Garis singgung dan jari-jari lingkaran di titik singgung berpotongan tegak lurus.

4. Dari satu titik di luar lingkaran, dapat dibentuk dua garis singgung yang sama panjang.

C. Lingkaran dan tali busur

Dalam matematika, ruas garis yang menghubungkan dua titik pada lingkaran disebut tali busur.

Pada segiempat tali busur berlaku:

1. Sudut-sudut yang berhadapan saling berpelurus.

2. Hasil kali diagonal sama besarnya dengan jumlah dari hasil kali sisi yang berhadapan.

Persamaan Umum Lingkaran

Persamaan umum lingkaran bisa ditentukan dengan sangat mudah. Perhatikan gambar berikut.

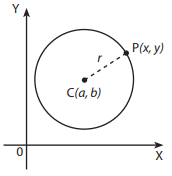
Gambar di atas menunjukkan bahwa terdapat suatu lingkaran yang berpusat di titik C dengan koordinat (a,b) dan berjari-jari r. Jari-jari merupakan jarak antara titik C dan P. Misalkan titik P(x,y) terletak di keliling lingkaran, sehingga jarak titik P ke pusat lingkaran dirumuskan sebagai berikut.

Persamaan di atas merupakan persamaan lingkaran dengan pusat C(a,b) dan jari-jari r.
Jika dijabarkan lebih lanjut, persamaan di atas akan menjadi:

Nah, persamaan (1) di atas merupakan persamaan umum lingkaran, dengan:

Dengan demikian, pusat dan jari-jari lingkarannya dinyatakan sebagai berikut.

Titik pusat lingkaran

Jari-jari lingkaran

Untuk mengasah kemampuan tentang Persamaan Umum Lingkaran, simak contoh soal berikut ini ya!

Contoh Soal 1

Tentukan persamaan umum lingkaran yang berpusat di (-3,4) dan menyinggung sumbu-Y!
Pembahasan:
Pertama-tama, gambarkan dahulu grafik lingkarannya, yaitu berpusat di (-3,4) dan menyinggung sumbu-Y!

Berdasarkan gambar di atas, terlihat bahwa pusat lingkarannya berada di koordinat (-3,4) dengan jari-jari 3, sehingga diperoleh:

Jadi, persamaan umum lingkaran yang berpusat di (-3,4) dan menyinggung sumbu-Y adalah 
Pada beberapa kasus, jari-jari lingkarannya tidak diketahui, tetapi garis singgungnya diketahui. Lantas bagaimana menentukan jari-jari lingkarannya? Perhatikan gambar berikut.

Gambar di atas menunjukkan bahwa garis singgung dengan persamaan px+  qy+ r= 0 menyinggung lingkaran yang berpusat di C(a,b). Untuk jari-jarinya bisa ditentukan dengan persamaan berikut.

Agar lebih paham tentang hubungan antara lingkaran beserta garis yang menyinggungnya, simak contoh soal 2 berikut ini.

Contoh Soal 2

Tentukan persamaan umum lingkaran yang berpusat di titik (5,1) dan menyinggung garis 3x– 4y+ 4 = 0!
Pembahasan:
Jika diketahui pusat lingkaran (a,b) = (5,1) dan garis singgung lingkarannya 3x– 4y+ 4 = 0, maka jari-jari lingkarannya dirumuskan sebagai berikut.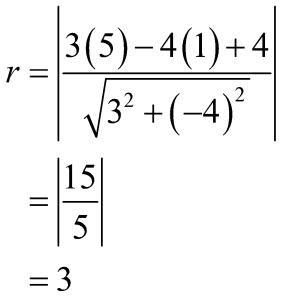

Dengan demikian, persamaan umum lingkarannya adalah sebagai berikut.

Jadi, persamaan umum lingkaran yang berpusat di titik (5,1) dan menyinggung garis 3x– 4y+ 4 = 0 adalah 

Hubungan Dua Buah Lingkaran

Sebelumnya, sudah belajar tentang titik pusat, jari-jari, serta persamaan umum untuk satu buah lingkaran. Bagaimana jadinya jika lingkarannya ada dua?

Misalnya, dua buah lingkaran L₁dengan pusat C₁, jari-jari r1dan lingkaran L₂dengan pusat C₂, jari-jari r₂memiliki hubungan sebagai berikut.

1. L₁ bersinggungan dalam dengan L₂

Perhatikan gambar berikut.

Berdasarkan gambar di atas, berlaku:

2. L₁ bersinggungan luar dengan L₂

Perhatikan gambar berikut.

Berdasarkan gambar di atas, berlaku:

3. L₁ di dalam L₂ tanpa bersinggungan

Perhatikan gambar berikut.

Berdasarkan gambar di atas, berlaku:

4. L₁ saling lepas dengan L₂

Perhatikan gambar berikut.

Berdasarkan gambar di atas, berlaku:

5. L₁ berpotongan dengan L₂

Perhatikan gambar berikut.

Berdasarkan gambar di atas, berlaku:

Kelihatannya rumit ya Quipperian, tetapi jangan khawatir karena Quipper Blog akan memberikan SUPER “Solusi Quipper” untuk mengingat hubungan antara dua buah roda.
Ini dia SUPERnya!

Tidak hanya itu, SUPER juga akan hadir untuk membantu Quipperian dalam mengingat jarak pusat C₁C₂, lho.

Apakah Quipperian sudah paham tentang hubungan antara dua buah lingkaran? Jika belum, coba simak contoh soal 3 berikut ini ya!

Contoh Soal 3

Tentukan hubungan antara lingkaran  dengan 
Pembahasan:
Pertama-tama, Quipperian harus mencari pusat dan jari-jari kedua lingkaran tersebut.
Jika ditinjau, lingkaran  memiliki nilai A= -10, B= 4, dan C= -167, sehingga pusat lingkarannya adalah

Jari-jari lingkarannya dirumuskan sebagai berikut.

Jika ditinjau, lingkaran  memiliki nilai A= 6, B= -16, dan C= 57, sehingga pusat lingkarannya adalah

Jari-jari lingkarannya dirumuskan sebagai berikut.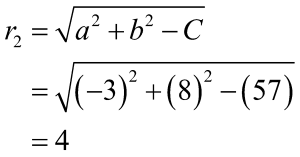

Setelah itu, Quipperian bisa menentukan nilai 

Oleh karena 10 < √164 < 18, maka lingkaran L₁berpotongan dengan lingkaran L₂.
Jadi, hubungan antar kedua lingkaran pada soal adalah saling berpotongan.
Setelah membaca ulasan tentang persamaan lingkaran di atas, apakah kalian sudah semakin paham? Pada dasarnya, banyak penerapan yang bisa gali setelah belajar tentang persamaan lingkaran ini, contohnya deteksi jangkauan radar, menentukan persamaan garis singgung pada hubungan roda-roda, menentukan persamaan lintasan pesawat tempur, dan masih banyak lainnya.
Jika Quipperian masih ingin mempelajari persamaan lingkaran secara intensif, silahkan gabung dengan Quipper Video, ya. Selamat belajar dengan tutor-tutor kece Quipper Video dan temukan ratusan soal di dalamnya.