Eksponen dan bentuk akar
- Dapatkan link
- X
- Aplikasi Lainnya
EKSPONEN (Bilangan berpangkat)
Pengertian bilangan berpangkat
Bilangan berpangkat , yaitu merupakan bilangan penyederhana dari sebuah bilangan yang di kalikan , atau untuk lebih memahaminya perhatikan penjelasan di bawah ini :
an = a x a x a x a x . . . .x n ( Sebanyak n )
Keterangan :
an = bilangan berpangkat
a = bilangan pokok
n = pangkat
Jenis – Jenis Bilangan Berpangkat
Bilangan berpangkat , terdiri dari beberapa jenis yaitu :
- Bilangan berpangkat bulat positif
yaitu merupakan penyederhanaan dari seatu perkalian bilangan bulat yang memiliki faktor yang sama .
Apabila dirumuskan adalah :
an = a x a x a x a x . . . .x n ( Sebanyak n )
Ket:
a = bilangan dasar ( bilangan pokok )
n = pangkat ( eksponen )
Contoh :
25 = 2 x 2 x 2 x 2 x 2 = 32
72 = 7 x 7 = 49
2. Bilangan Berpangkat bulat negatif
Yaitu merupakan bilangan yang pangkatnya merupakan bilangan negatif .
Apabila dirumuskan :
Contoh :
10-2 = 1 / 102
3. Bilangan Berpangkat Nol
Yaitu merupakan bilangan berpangkat yang pangkatnya nol . Dan semua bilangan yang di pangkatkan nol hasilnya 1.
Apabila dirumuskan :
a0 = 1
C. Sifat – sifat Bilangan Berpangkat
Untuk dapat megerjakan permasalahan – permasalahan di dalam soal bilangan berpangkat , kita harus mengetahui sifat – sifat bilangan berpangkat supaya kita dalam mengerjakannya kita memiliki tata aturan dasar atau sebagai pacuan dalam mengerjakannya dan supaya mempermudah dalam mengerjakannya .
Sifat – sifat bilangan berpangkat adalah sebagai berikut :
- Perkalian Bilangan Berpangkat
Dalam perkalian bilangan berpangkat , maka berlaku sifat seperti di bawah ini :
Contoh :
- 22 x 26 = 2 2+6 = 28
- 32 x 32 = 2 2+2 = 24
2. Pembagian Bilangan Berpangkat
Dalam pembagian bilangan berpangkat berlaku rumus :
Contoh :
- 36 : 32 = 2 6-2 = 24
- 66 : 63 = 66-3 = 63
3. Sifat Pemangkatan Bilangan Berpangkat
Apabila ada suatu bilangan berpagkat yang di pangkatkan lagi ,maka berlaku rumus :
(am)n = a m x n
Contoh :
( 23 ) 2 = 2 3 x 2 = 26
4. Sifat Perpangkatan Suatu Perkalian atau pembagian
- Apabila ada dua bilangan bulat yang dikalikan dan di pangkatkan maka berlaku rumus :
( a x b ) n = an x bn
- Apabila ada dua bilangan bulat yang di bagi dan di pangkatkan maka berlaku rumus :
( a : b ) n = an : bn
Contoh Soal
- Sederhanakan bentuk bilangan berpangkat berikut :
Penyelesaian :
< = >( P6 / q -9 ) ( 4q2 /p6 )
< = >( P6 : 1/ q 9 ) (4q2 . p-6 )
< = > (P6 . q 9 ) (4q2 . p-6 )
< = > 4. P6 + (-6) . q 9+2
<= > 4. P0 . q 11
< = > 4.1. q 11
< = > 4 q 11
< = > 2x3 : x -2 + 4x6 : x -2
< = > 2x3 : 1/ x2 + 4x6 : 1/ x2
< = > 2x3 . x2 + 4x6 . x 2
< = > 2 x3 + 2 + 4 x6 + 2
< = > 2 x5 + 4x8
2. Tentukan hasil dari bentuk pangkat berikut :
a. 53 x 54
b. ( -3 ) 6 x ( -3 ) 9
c. ( – 2 ) 10 x ( -2 ) 20
d. a10 x a20 x a30
Penyelesaian :
a. 53x 54 = 5 3+ 4 = 57
b. ( -3 )6x ( -3 )9 = ( – 3 ) 6 + 9 = ( – 3 ) 15
c. ( – 2 )10x ( -2 ) 20 = ( -2 ) 10 + 20 = ( -2 ) 30
d. a10x a20x a30 = a 10 + 20 + 30 = a 60
BENTUK AKAR
Bentuk akar merupakan salah satu contoh bilangan irrasional. Bentuk ini pada awalnya sering diasumsikan sebagai produk dari teorema Pythagoras.
Sebagai contoh:
Sebagai contoh:
Dalam hal ini berlaku : Untuk a dan n adalah bilangan real tak negatif , maka
Bentuk akar dibagi dalam dua jenis, yakni
1. bentuk akar murni, misalnya
2. bentuk akar campuran yang merupakan hasil perkalian antara bilangan rasional dan irrasional, misalnya.
Namun beberapa bentuk akar dapat disederhanakan, seperti diuraikan pada contoh-contoh soal berikut ini
01. Sederhanakanlah
Jawab

Sifat-sifat operasi aljabar pada bentuk akar
Untuk a dan b bilangan real tak negatif serta m dan n adalah bilangan real sembarang, maka berlaku :
Jawab
04. Sederhanakanlah
Jawab

Cara lain menyederhanakan bentuk akar adalah menyederhanakan bentuk pecahan yang memuat akar. Prosesnya adalah dengan merasionalkan penyebut pecahan
Merasionalkan penyebut pecahan dapat dilakukan dengan cara mengalikan pembilang dan penyebut dengan suatu bentuk tertentu sehingga penyebut pecahan tersebut menjadi rasional. Terdapat dua bentuk pengali dalam hal ini, yaitu :
Bentuk 1
Untuk memahami uraian di atas, ikutilah contoh-contoh soal berikut ini
01. Sederhanakanlah
Jawab
Sebelum membahas bentuk 2, terlebih dahulu akan dikenalkan bentuk akar konjugat dari suatu bentuk akar, yakni :
Jika hasil kali dua bentuk akar adalah bilangan rasional, maka masing-masing dari kedua bentuk akar tersebut dinamakan faktor rasional atau bentuk akar konjugat dari bentuk akar yang lain
Dengan adanya bentuk konjugat ini, maka bentuk 2 dapat dirumuskan sebagai:
Bentuk 2
Sebagai contoh :
01. Sederhanakanlah setiap bentuk akar berikut ini :
Jawab

02. Sederhanakanlah setiap bentuk akar berikut ini :
Jawab
Demikian penjelasan mengenai Pengertian dan sifat eksponen (bilangan berpangkat) dan bentuk akar, Intinya , dalam bilangan berpangkat dan bentuk akar, ada hubungan antara penjumlahan , pengurangan, perkalian dan pembagian . Dan supaya dalam mengerjakan soal bilangan berpangkat dan bentuk akar menjadi lebih mudah , maka anda semua harus memahami betul mengenai sifat – sifat bilangan berpangkat dan bentuk akar, Jika kalian sudah memahaminya, maka di buat dalam bentuk apa pun akan terasa mudah . Semoga dengan penjelasan dan contoh di atas , kita semua akan bertambah ilmunya, Serta dapat membantu permasalahan dalam materi bilangan berpangkat,
Selamat belajar....salam 😉
- Dapatkan link
- X
- Aplikasi Lainnya

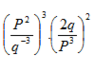
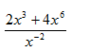










Komentar
Posting Komentar