Rumus Jumlah dan Selisih Dua Sudut Sin, Cos, dan Tg

April 19, 2020

Fungsi dari Rumus Jumlah dan Selisih Dua Sudut Sinus, Cosinus, dan Tangen digunakan untuk menentukan nilai sudut yang tidak ada dalam sudut istimewa. Sebelumnya, pasti sudah tahu bagaimana cara menentukan nilai sudut istimewa. Ada dua cara yang digunakan untuk memudahkan kita mengingat nilai dari sudut istimewa. Cara pertama adalah menggunakan grafik fungsi sinus atau grafik gungsi cosinus. Cara kedua adalah mengggunakan rumus identitas trigonometri. Tabel lengkap nilai trigonometri dapat dilihat pada halaman ini. Sekarang, mari kita simak rumus jumlah dan selisih dua sudut sinus dan cosinus beserta pembuktiannya.

Rumus Jumlah dan Selisih Sudut Cosinus

Rumus Jumlah Sudut Cosinus

Bukti:
Perhatikan gambar berikut!

Pembuktian Rumus Jumlah Sudut Cos

Titik koordinat A dan B di atas diperoleh berdasarkan fungsi sinus dan cosinus. Selanjutnya perhatikan titik M yang ditransformasi dengan besar sudut putar $\beta$ dan sudut pusat O dari titik A. Dan perhatikan titik N yang ditransformasi dengan besar sudut putar $- \beta$ dan sudut pusat O dari titik P. Untuk lebih jelasnya perhatikan gambar di bawah.

INGAT!!!

$cos (-\alpha) = cos \alpha$

$sin (-\alpha) = - sin \alpha$

Persamaan 1: Menghitung jarak P(1,0) ke M (cos $( \alpha + \beta)$ , sin $( \alpha + \beta)$ )

$\left| PM \right| = \sqrt{\left( x_{P} - x_{M} \right)^{2} + \left( y_{P} - y_{M} \right)^{2}}$

$\left| PM \right| = \sqrt{\left( 1 - cos \left( \alpha + \beta \right) \right)^{2} + \left( 0 - sin \left( \alpha + \beta \right) \right)^{2}}$

$\left| PM \right| = \sqrt{1 - 2cos \left( \alpha + \beta \right) + cos^{2} \left( \alpha + \beta \right) + sin^{2} \left( \alpha + \beta \right)}$

$\left| PM \right| = \sqrt{1 - 2cos \left( \alpha + \beta \right) + 1}$

$\left| PM \right| = \sqrt{2 - 2cos \left( \alpha + \beta \right)}$

Persamaan 2: Menghitung jarak A $(cos \alpha, sin \alpha)$ ke N $(cos \beta, -sin \beta)$

$\left| AN \right| = \sqrt{\left( x_{A} - x_{N} \right)^{2} + \left( y_{A} - y_{N} \right)^{2}}$

$\left| AN \right| = \sqrt{\left( cos \alpha - cos \beta \right)^{2} + \left( sin \alpha - (-sin \beta) \right)^{2}}$

$\left| AN \right| = \sqrt{\left( cos \alpha - cos \beta \right)^{2} + \left( sin \alpha + sin \beta \right)^{2}}$

$\left| AN \right| = \sqrt{cos^{2} \alpha - 2cos \alpha cos \beta + cos^{2} \beta + sin^{2} \alpha + 2sin \alpha sin \beta + sin^{2} \beta}$

$\left| AN \right| = \sqrt{cos^{2} \alpha + sin^{2} \alpha + cos^{2} \beta + sin^{2} \beta} + - 2cos \alpha cos \beta + 2sin \alpha sin \beta$

$\left| AN \right| = \sqrt{1 + 1 - 2cos \alpha cos \beta + 2sin \alpha sin \beta}$

$\left| AN \right| = \sqrt{2 - 2cos \alpha cos \beta + 2sin \alpha sin \beta}$

Secara geometri, persamaan 1 sama dengan persamaan 2, sehingga:

$\left| PM \right| = \left| AN \right|$

$\sqrt{2 - 2cos \left( \alpha + \beta \right)} = \sqrt{2 - 2cos \alpha cos \beta + 2sin \alpha sin \beta}$

$2 - 2cos \left( \alpha + \beta \right) = 2 - 2cos \alpha cos \beta + 2sin \alpha sin \beta$

$- 2cos \left( \alpha + \beta \right) = - 2cos \alpha cos \beta + 2sin \alpha sin \beta$

$cos \left( \alpha + \beta \right) = cos \alpha cos \beta - sin \alpha sin \beta$

Terbukti

Contoh Soal Penggunaan Rumus Jumlah Sudut Cosinus
Tentukan nilai cos $75^{o}$ !
Pembahasan:

$cos \; 75^{o} = cos \left( 45^{o} + 30^{o} \right)$

$cos \; 75^{o} = cos \; 45^{o} \cdot cos \; 30^{o} - sin \; 45^{o} \cdot sin \; 30^{o}$

$cos \; 75^{o} = \frac{1}{2} \sqrt{2} \cdot \frac{1}{2} \sqrt{3} - \frac{1}{2} \sqrt{2} \cdot \frac{1}{2}$

$cos \; 75^{o} = \frac{1}{4} \sqrt{6} - \frac{1}{4} \sqrt{2}$

$cos \; 75^{o} = \frac{1}{4} \left( \sqrt{6} - \sqrt{2} \right)$

Rumus Selisih Sudut Dua Cosinus

Rumus Selisih Dua Sudut Cos

Pembuktian rumus di atas dapat diperoleh dengan memanfaatkan rumus jumlah sudut cosinus yang telah kita buktikan terlebih dahulu. Caranya adalah dengan mengubah sudut $\beta$ menjadi sudut $- \beta$ . Untuk lebih jelasnya lihat langkah pembuktian di bawah.

Bukti:

$cos \left( \alpha - \beta \right) = cos \left( \alpha + (- \beta) \right)$

$cos \left( \alpha - \beta \right) = cos \alpha \cdot cos (- \beta) - sin \alpha \cdot sin (- \beta)$

$cos \left( \alpha - \beta \right) = cos \alpha \cdot cos \beta - sin \alpha \cdot -sin \beta$

$cos \left( \alpha - \beta \right) = cos \alpha \; cos \beta + sin \alpha \; sin \beta$

Terbukti

Contoh Soal Penggunaan Rumus Selisih Dua Sudut Cosinus
Tentukan nilai cos $75^{o}$ !
Pembahasan:

$cos \; 105^{o} = cos \left( 135^{o} - 30^{o} \right)$

$cos \; 105^{o} = cos \; 135^{o} \cdot cos \; 30^{o} - sin \; 135^{o} \cdot sin \; 30^{o}$

$cos \; 105^{o} = -\frac{1}{2} \sqrt{2} \cdot \frac{1}{2} \sqrt{3} - \frac{1}{2} \sqrt{2} \cdot \frac{1}{2}$

$cos \; 105^{o} = -\frac{1}{4} \sqrt{6} - \frac{1}{4} \sqrt{2}$

$cos \; 105^{o} = -\frac{1}{4} \left( \sqrt{6} - \sqrt{2} \right)$

Rumus Jumlah dan Selisih Dua Sudut Sinus

Rumus Jumlah Dua Sudut Sinus

Bukti:

$sin \left( \alpha + \beta \right) = cos \left( 90^{o} - (\alpha + \beta) \right)$

$sin \left( \alpha + \beta \right) = cos \left( (90^{o} - \alpha) - \beta \right)$

$sin \left( \alpha + \beta \right) = cos (90^{o} - \alpha) \cdot cos \beta + sin (90^{o} - \alpha) \cdot sin \beta$

$sin \left( \alpha + \beta \right) = sin \alpha \; cos \beta + cos \alpha \; sin \beta$

Contoh Soal Penggunaan Rumus Jumlah Sudut Sinus
Tentukan nilai dari $sin 105^{o} cos 75^{o} + cos 105^{o} sin 75^{o}$ !
Pembahasan:

$sin 105^{o} cos 75^{o} - cos 105^{o} sin 75^{o} = sin (105^{o} + 75^{o}$

$sin 105^{o} cos 75^{o} - cos 105^{o} sin 75^{o} = sin (180^{o}) = 0$

Rumus Selisih Dua Sudut Sinus

Bukti:

$sin \left( \alpha - \beta \right) = sin \left( \alpha + (- \beta) \right)$

$sin \left( \alpha - \beta \right) = cos \left( 90^{o} - (\alpha + (- \beta)) \right)$

$sin \left( \alpha - \beta \right) = cos \left( (90^{o} - \alpha) + \beta) \right)$

$sin \left( \alpha - \beta \right) = cos (90^{o} - \alpha) \cdot cos \beta - sin (90^{o} - \alpha) \cdot sin \beta$

$sin \left( \alpha - \beta \right) = sin \; \alpha \; cos \; \beta - cos \; \alpha \; sin \; \beta$

Contoh Soal Penggunaan Rumus Selisih Sudut Sinus
Tentukan nilai dari $sin 105^{o} cos 75^{o} + cos 105^{o} sin 75^{o}$ !
Pembahasan:

$sin 105^{o} cos 75^{o} - cos 105^{o} sin 75^{o} = sin (105^{o} - 75^{o}$

$sin 105^{o} cos 75^{o} - cos 105^{o} sin 75^{o} = sin (30^{o}) = \frac{1}{2}$

Rumus Jumlah dan Selisih Sudut Tangen

Rumus Jumlah Sudut Tangen

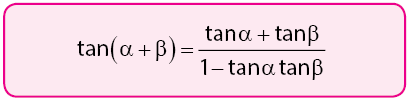
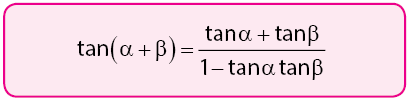
Rumus Jumlah Dua Sudut Tan

Bukti:

$tan(\alpha + \beta ) = \frac{sin(\alpha + \beta)}{cos(\alpha + \beta)}$

$tan(\alpha + \beta ) = \frac{sin \alpha \; cos \beta + cos \alpha \; sin \beta}{cos \alpha \; cos \beta - sin \alpha \; sin \beta}$

$tan(\alpha + \beta ) = \frac{\frac{sin \alpha}{cos \alpha} \cdot cos \alpha \; cos \beta + cos \alpha \; \frac{sin \beta}{cos \beta} \cdot cos \beta}{cos \alpha \; cos \beta - \frac{sin \alpha}{cos \alpha} \cdot cos \alpha \; \frac{sin \beta}{cos \beta} \cdot cos \beta}$

$tan(\alpha + \beta ) = \frac{tan \alpha \; cos \alpha \; cos \beta + cos \alpha \; tan \beta \; cos \beta}{cos \alpha \; cos \beta - tan \alpha \; cos \alpha \; tan \beta \; cos \beta }$

$tan(\alpha + \beta ) = \frac{cos \alpha \; cos \beta \left( tan \alpha + tan \beta \right)}{cos \alpha \; cos \beta \left( 1 - tan \alpha \; tan \beta \right)}$

$tan(\alpha + \beta ) = \frac{tan \alpha + tan \beta }{ 1 - tan \alpha \; tan \beta}$

Terbukti

Contoh perhitungan jumlah sudut Tangen
Diketahui:

$tan \; \beta \; = \; \frac{5}{4}$

$\left( \alpha + \beta \right) = 315^{o}$

Maka nilai $tan\; \alpha$ adalah ….

$A. \; \; \; 9$

$B. \; \; \; \frac{9}{2}$

$C. \; \; \; 3$

$D. \; \; \; \frac{9}{4}$

$E. \; \; \; \frac{9}{7}$

Pembahasan:

$tan \; (\alpha + \beta) = \frac{tan \; \alpha + tan \; \beta}{1-tan \; \alpha tan \; \beta}$

$tan \; 315^{o} = \frac{tan \; \alpha + \frac{5}{4}}{1- tan \; \alpha \cdot \frac{5}{4}}$

$-1 = \frac{tan \; \alpha + \frac{5}{4}}{1- \frac{5}{4}tan \; \alpha}$

$-1\left(1- \frac{5}{4}tan \; \alpha \right) = tan \; \alpha + \frac{5}{4}$

$-1+ \frac{5}{4}tan \; \alpha = tan \; \alpha + \frac{5}{4}$

$\frac{5}{4}tan \; \alpha - tan \; \alpha = \frac{5}{4} + 1$

$\frac{1}{4}tan \; \alpha = \frac{9}{4} \rightarrow tan \; \alpha = 9$

Jawaban: A

Rumus Selisih Sudut Tangen

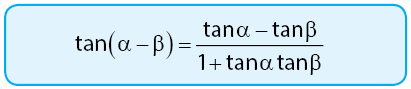
Rumus Selisih Dua Sudut Tan

Bukti:

Dengan menggunakan rumus jumlah sudut tangen yang telah di buktikan sebelumnya, pembuktian rumus selisih sudut tangen dapat diperoleh dengan mengganti sudut $\beta$ menjadi $- \beta$ .

$tan(\alpha - \beta ) = tan(\alpha + (-\beta))$