Nilai mutlak

Persamaan nilai mutlak 



Pengertian nilai mutlak 

Nilai mutlak merupakan suatu jarak antara bilangan tertentu dengan nol pada garis bilangan real. Karena jarak, maka nilainya selalu positif (tidak ada yang negatif). Sehingga nilai mutlak yaitu nilai yang selalu positif.

Konsep nilai mutlak digunakan pada Selisih bilangan selalu dianggap positif karena itu konsep nilai mutlah berlaku (digunakan) pada hitungan selilih bilangan.

Jarak suatu benda selalu dianggap positif karena konsep nilai mutlak digunakan pada hitungan jarak benda, Toleransi resistor (perubahan nilai resistansi), begitu juga dengan galat pengukuran juga menggunakan konsep nilai mutlak.

Untuk memahami konsep nilai mutlak, akan diilustrasikan dengan cerita berikut ini: Seorang anak pramuka sedang latihan baris berbaris. Dari posisi diam, si anak diminta maju 2 langkah ke depan, kemudian 4 langkah ke belakang. Dilanjutkan dengan 3 langkah ke depan dan akhirnya 2 langkah ke belakang. Dari cerita di atas dapat diambil permasalahan :

a. Berapakah banyaknya langkah anak pramuka tersebut dari pertama sampai terakhir ?
b. Dimanakah posisi terakhir anak pramuka tersebut, jika diukur dari posisi diam? (berapa langkah ke depan atau berapa langkah ke belakang)

Untuk menjawab permasalahan diatas, akan diberikan gambar garis bilangan berikut:

Dari gambar di atas, kita misalkan bahwa x = 0 adalah posisi diam (awal) si anak. Anak panah ke kanan menunjukkan arah langkah ke depan (bernilai positif) dan anak panah ke kiri menunjukkan arah langkah ke belakang (bernilai negatif). Sehingga permasalahan di atas dapat dijawab sebagai berikut :

a. Banyaknya langkah anak pramuka tersebut dari pertama sampai terakhir adalah Bentuk penjumlahan 2 + 4 + 3 + 2 = 11 langkah. Bentuk penjumlahan ini merupakan penjumlahan tampa memperhatikan arah ke depan (positif) dan ke belakang (negatif)

b. Dari gambar diatas, dapat dilihat bahwa posisi terakhir anak pramuka tersebut, jika diukur dari posisi diam adalah 1 langkah ke belakang (x = –1). Hasil ini didapat dari bentuk penjumlahan 2 + (–4) + 3 + (–1) = –1. Bentuk penjumlahan ini merupakan penjumlahan dengan memperhatikan arah ke depan (positif) dan ke belakang (negatif).


Ilustrasi dari penyelesaian soal (a) di atas merupakan dasar dari konsep nilai mutlak. Dimana Nilai mutlak suatu bilangan real x merupakan jarak antara bilangan itu dengan nol pada garis bilangan. Dan dilambangkan dengan │x│. Secara formal nilai mutlak didefinisikan


Dari konsep diatas diperoleh : 
│–3│ = 3 , │–15│ = 15 , │6│ = 6 , │10│ = 10 dan seterusnya.
Untuk lebih memahami pertidaksamaan nilai mutlak, perhatikan contoh berikut :

01. Tentukanlah nilai
(a) │–4│ + │5│ – │–3│    (b) 6 – │–2│ + │–5│ + 1
(c) │4 – │–7││                   (d) │–9 + │–2││

Jawab
(a) │–4│ + │5│ – │–3│ = 4 + 5 – 3 = 6
(b) 6 – │–2│ + │–5│ + 1 = 6 – 2 + 5 + 1 = 10
(c) │4 – │–7││ = │4 – 7│ = │–3│ = 3
(d) │–9 + │–2││ = │–9 + 2│ =│–7│ = 7

02. Untuk x = –3, maka tentukanlah nilai │x2 + 6x + 5│

Jawab
│x2 + 6x + 5│ = │(–3)2 + 6(–3) + 5│
                         = │9 – 18 + 5│
                         = │–4│ 
                         = 4

03. Untuk x = 2, maka tentukanlah nilai 
        4│2 – 6x│+ │3x – 8│

Jawab
4│2 – 6x│+ │3x – 8│ = 4│2 – 6(2)│+ │3(2) – 8│
                                      = 4│–10│+ │–2│
                                      = 40 + 2
                                      = 42

04. Untuk x = –2, maka tentukanlah nilai
       │x2 – 6x│– │4x + 5│

Jawab
│x2 – 6x│– │4x + 5│= │(–2)2 – 6(–2)│– │4(–2) + 5│
                                     = │4 + 12│– │–8 + 5│
                                     = 16 + 3
                                     = 19

05. Seekor bekicot akan menaiki tiang bendera dimulai awal tanggal 5 Agustus. Jika pada tanggal ganjil bekicot itu bergerak naik setinggi 5 m, dan pada tanggal genap ia turun sejauh 3 m, maka ia akan tiba dipuncak tiang bendera tepat pada akhir tanggal 17 Agustus.
(a) Berapakah tinggi tiang bendera
(b) Berapakah jauh perjalanan bekicot itu?

Jawab
(a) Tinggi tiang bendera = 5 – 3 + 5 – 3 + 5 – 3 + 5 – 3 + 5 – 3 + 5 – 3 + 5 = 17m
(b) jauh perjalanan bekicot itu =
 5 + │–3│ + 5 + │–3│+ 5 + │–3│+ 5 + │–3│+ 5 + │–3│ + 5 + │–3│+ 5 = 53 m

Untuk menyelesaikan persamaan nilai mutlak, dapat digunakan sifat
01. (a) Jika │f(x)│ = a maka f2(x) = a2
(b) Jika │f(x)│ = a maka f(x) = a atau f(x) = –a

02. (a) Jika │f(x)│ = │g(x)│ maka f2(x) = g2(x) 
(b) Jika │f(x)│ = │g(x)│ maka f(x) = g(x) atau f(x) = –g(x)

Untuk lebih memahami pertidaksamaan nilai mutlak, perhatikan contoh berikut :
01. Tentukan nilai x yang memenuhi persamaan berikut :
(a) │2x – 5│ = 3                  (b) │4 – 3x│ = 6

Jawab
(a) │2x – 5│ = 3
(2x – 5)2 = 32
4x2 – 20x + 25 = 9
4x2 – 20x + 16 = 0
x2 – 5x + 4 = 9
(x – 4)(x – 1) = 0
Jadi x = 1 dan x = 4

(b) │3 – 2x│ = 7
(3 – 2x)2 = 72
9 – 12x + 4x2 = 49
4x2 – 12x – 40 = 0
x2 – 3x – 10 = 0
(x – 5)(x + 2) = 0
Jadi x = 5 atau x = –2

02. Tentukan nilai x yang memenuhi persamaan berikut :
(a) │2x + 4│ = │x – 1│                    (b) │3x + 4│ = │2x – 1│

Jawab
(a) │2x + 4│ = │x – 1│
(2x + 4)2 = (x – 1)2
4x2 –16x + 16 = x2 – 2x + 1
3x2 – 14x + 15 = 0
(3x – 5)(x – 3) = 0
Jadi x = 5/3 atau x = 3

(b) │3x + 4│ = │2x – 1│
(3x + 4)2 = (2x – 1)2
9x2 +24x + 16 = 4x2 – 4x + 1
5x2 + 28x + 15 = 0
(5x + 3)(x + 5) = 0
Jadi x = –3/5 atau x = –5

03. Tentukan nilai x yang memenuhi persamaan berikut :
(a) │3x – 2│ = x + 4                          (b) │2x + 4│ = x – 3

Jawab
(a) │3x – 2│ = x + 4
(3x – 2)2 = (x + 4)2
9x2 – 12x + 4 = x2 + 8x + 16
8x2 – 20x – 12 = 0
2x2 – 5x – 3 = 0
(2x + 1)(x – 3) = 0
Jadi x = –1/2 atau x = 3

Uji: x = –1/2 maka x + 4 = –1/2 + 4 = 7/2 (memenuhi)
Uji: x = 3 maka x – 4 = 3 + 4 = 7 (memenuhi)
Sehingga H = {–1/2, 3}

(b) │2x – 4│ = x – 3
(2x – 4)2 = (x – 3)2
4x2 –16x + 16 = x2 – 6x + 9
3x2 – 22x + 7 = 0
(3x – 1)(x – 7) = 0
Jadi x = 1/3 atau x = 7

Uji: x = 1/3 maka x – 3 = 1/3 – 4 = –11/3 (tidak memenuhi)
Uji: x = 7 maka x – 4 = 7 – 4 = 3 (memenuhi)
Sehingga H = {7}



Pertidaksamaan Nilai Mutlak


Pembahasan materi pertidaksamaan nilai mutlak biasanya meliputi cara menentukan nilai yang memnuhi pertidaksamaan nilai mutlak. Nilai yang memenuhi tersebut biasanya dinyatakan dalam himpunan penyelesaian. Dalam meyelesaikan pertidaksamaan nilai mutlak dibutuhkan pertidaksamaan bentuk aljabar yang ekuivalen dengan pertidaksamaan tersebut. Kumpulan pertidaksamaan bentuk aljabar yang ekuivalen dengan pertidaksamaan nilai mutlak diberikan dalam sifat pertidaksamaan nilai mutlak, yang akan diulas kemudian.
Melalui sifat pertidaksamaan nilai mutlak tersebut, sobat dapat menentukan himpunan penyelesaian dari soal pertidaksamaan nilai mutlak yang diberikan.
Melalui halaman ini, sobat idschool dapat mempelajari pertidaksamaan aljabar yang ekuivelan dengan pertidaksamaan nilai mutlak. Sehingga, sobat kemudian dapat menentukan himpunan penyelesaian dari pertidaksamaan nilai mutlak. Penggunaannya dapat dilihat pada cara menyelesaiakan pertidaksamaan nilai mutlak untuk mendapatkan himpunan penyelesaiannya, akan diberikan pada akhir pembahasan. Jadi, simak terus sampai akhir. Oke?!
Sebelum membahas pertidasakaam nilai mutlak, akan dijelaskann terlebih dahulu tentang fungsi nilai mutlak. Tanda nilai mutlak disimbolkan dengan dua buah garis yang mengapit seuatu persamaan. Jika nilai di dalam tanda mutlak lebih besar dari nol maka nilai fungsinya adalah positif. Kondisi sebaliknya juga berlaku, jika nilai di dalam tanda mutlak lebih kecil dari nol maka nilai fungsinya adalah negatif. Sedangkan jika nilai yang diberikan dalam tanda adalah nol maka nilainya juga akan nol.
Dalam bahasa sederhananya, tanda mutlak akan selalu membuat nilai yang berada dalam tanda tersebut selalu bernilai positif. Seperti terlihat pada fungsi yang diberikan di bawah.
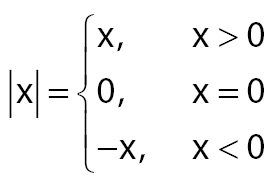
Nilai Mutlak
Dengan fungsi yang diberikan seperti di atas akan menghasilkan nilai yang selalu positif. Bagaimana? Cukup mudah dimengerti, bukan? Untuk memperjelas penjelasan tentang nilai mutlak akan diberikan uraian pengantar nilai mutlak dan sifat pertidaksamaan nilai mutlak.
Nantinya, materi ini akan berguna untuk menentukan berbagai solusi dari permasalah-permasalahan yang melibatkan fungsi nilai mutlak. Ingat! Pada bagian akhir, akan diberikan contoh soal pertidaksamaan nilai mutlak beserta dengan pembahasannya.
Simak ulasan pertama yang akan diberikan di bawah, yaitu pengantar nilai mutlak.

Pengantar Nilai Mutlak

Pada pembahasan sebelumnya di atas telah disinggung sedikit bahwa nilai mutlak diperoleh dengan mengambil nilai positif yang dapat dihasilkan oleh fungsi tersebut. Fungsi nilai mutlak meupakan fungsi yang kontinu. Jika digambarkan dalam bentuk grafik, gambar grafik fungsi nilai mutlak membentuk garis lurus, seperti membentuk huruf v pada interval tertentu. Grafik yang dihasilkan mempunyai satu buah titik puncak dan garisnya simetris, antara ruas kanan dan kiri.
Perhatikan gambar grafik nilai mutlak yang diberikan seperti gambar di bawah.
Gambar Grafik Fungsi Nilai Mutlak
Cukup mudah dipahami, bukan? Dan seperti yang terlihat pada kasusu di atas bahwa nilai fungsi nilai mutlak selalu positif (di atas sumbu x).
Demikianlah tadi, sedikit ulasan tentang pengatar nilai mutlak dalam bentuk persamaan. Selanjutnya adalah ulasan materi tentanng sifat pertidaksamaan nilai mutlak. Simak sifat-sifatnya yang akan diberikan pada ulasan di bawah.

Sifat Pertidaksamaan Nilai Mutlak

Mengambil nilai mutlak dari persamaan nilai mutlak cukup mudah. Dengan mengikuti dua aturan penting seperti yang telah dibahas sebelumnya sudah dapat menentukan nilai mutlaknya. Intinya, nilainya akan positif jika fungsi di dalam tanda mutlak lebih dari nol. Dan akan bernilai negatif jika fungsi di dalam tanda mutlak kurang dari nol.
Dalam pertidaksamaan nilai mutlak tidak cukup dengan cara demikian. Ada pertidaksamaan aljabar yang ekuivalen dengan pertidaksamaan nilai mutlak. Atau dapat disebut saja sebagai sifat pertidaksamaan nilai mutlak. Sifat inilah yang dapat digunakan untuk menentukan himpunan penyelesaian pada soal-soal pertidaksamaan nilai mutlak yang diberikan.
Berikut ini adalah sifat-sifat pertidaksamaan nilai mutlak yang dapat digunakan untuk menyekesaikan soal-soal terkait pertidaksmaan nilai mutlak.
Pertidaksamaan Nilai Mutlak
Dalam menyelesaikan pertidaksamaan nilai mutlak, selain perlu mengetahui sifa-sifat yang telah diberikan di atas, diperlukan juga kemampuan untuk menguasai cara operasi bentuk aljabar. Cara dasar dalam mengoperasikan bilangan dan variabel.
Untuk menambah pemahaman squad tentang cara menyelesaikan soal pertidaksamaan nilai mutlak dan cara menentukan himpunan penyelesaiannya, akan diberikan contoh soal pertidaksamaan nilai mumtlak yang dapat disimak pada contoh soal – contoh soal pertidaksamaan nilai beserta pembahasannya yang diberikan pada ulasan di bawah.

Contoh Soal dan Pembahasan

Contoh Soal Pertidaksamaan Nilai Mutlak Bentuk \left | ax+b \right | < c
Himpunan penyelesaian pertidasamaan mutlak berikut
  \[ \left | 2x + 5 \right | < 17 \]
adalah ….
  \[ \textrm{A.} \; \; \; \; - 11 < x < 6 \]
  \[ \textrm{B.} \; \; \; \; x < -11 \; \textrm{atau} \; x > 6 \]
  \[ \textrm{C.} \; \; \; \; -22 < x < 12 \]
  \[ \textrm{D.} \; \; \; \; -6 < x < 11 \]
  \[ \textrm{E.} \; \; \; \; x < -6 \; \textrm{atau} \; x > 11 \]
Pembahasan:
  \[ \left | 2x + 5 \right | < 17 \]
Berdasarkan pertidaksamaan nilai mutlak, akan diperoleh persamaan di bawah.
  \[ -17 < 2x + 5 < 17 \]
  \[ -17 -5 < 2x < 17 - 5 \]
  \[ -22< 2x < 12 \]
  \[ - \frac{22}{2}< x < \frac{12}{2} \]
  \[ - 11 < x < 6 \]
Jadi, himpunan penyelsaian yang sesuai untuk pertidaksamaan \left | 2x + 5 \right | < 17 adalah - 11 < x < 6.
Jawaban: A
Contoh Soal Pertidaksamaan Nilai Mutlak Bentuk \left | f(x) \right | > \left | g(x) \right |
Himpunan penyelesaian pertidasamaan mutlak berikut
  \[ \left | x + 5 \right | > \left | x - 2 \right | \]
adalah ….
  \[ \textrm{A.} \; \; \; \; 0 < x < - \frac{3}{2} \]
  \[ \textrm{B.} \; \; \; \; x < \frac{3}{2} \]
  \[ \textrm{C.} \; \; \; \; x > \frac{3}{2} \]
  \[ \textrm{D.} \; \; \; \; x < - \frac{3}{2} \]
  \[ \textrm{E.} \; \; \; \; x > - \frac{3}{2} \]
Pembahasan:
Berdasarkan ketentuan pada pertidaksamaan nilai mutlak, diperoleh pertidaksamaan berikut.
  \[ \left ( x + 5 \right ) ^{2} > \left ( x - 2 \right ) ^{2} \]
  \[ x^{2} + 10x +25 > x^{2} - 4x + 4 \]
  \[ x^{2} - x^{2} + 10x + 4x +25 - 4 > 0 \]
  \[ 14x + 21 > 0 \]
  \[ 14x > -21 \]
  \[ x > - \frac{21}{14} \]
  \[ x > - \frac{3}{2} \]
Sehingga himpunan penyelesaian pertidasamaan mutlak \left | x + 5 \right | > \left | x - 2 \right | adalah x > - \frac{3}{2}.
Jawaban: E
Demikianlah ulasan materi tentang nilai mutlak. Meliputi persamaan nilai mutlak, sifat persamaan nilai mutlak, pengantar nilai mutlak, sifat pertidaksamaan nilai mutlak, dan contoh soal persamaan dan pertidaksamaan nilai mutlak berserta dengan pembahasannya. Terimakasih sudah mengunjungi atikroest.blogspot.com semoga bermanfaat

Komentar

Posting Komentar

Postingan populer dari blog ini

Kesebangunan dan Kekongruenan (soal dan pembahasan)

Gambar
Kesebangunan dan Kekongruenan Hallo sobat atikroest, pada halaman ini akan mengupas tentang contoh soal kesebangunan dan kekongruenan. Seperti kisi-kisi yang telah dikeluarkan BSNP, materi kesebangunan dan kekongruenan akan kembali muncul di ujian nasional. Kisi-kisi untuk kesebangunan dan kekongruenan diberikan dalam 3 (tiga) level kognitif, yaitu pengetahuan dan pemahaman, aplikasi, dan penalaran. Halaman ini akan membahas kisi-kisi UN 2019 dengan materi kesebangunan dan kekongruenan untuk level pengetahuan dan pemahaman. Simak kumpulan soal UN dengan materi kesebangunan dan kekongruenan pada pembahasan di bawah. BAGIAN I Contoh 1: Soal UN Matematika SMP/MTS Tahun 2014 Perhatikan gambar! Banyak pasangan segitiga yang kongruen adalah …. A.     1 B.     2 C.     3 D.     4 Pembahasan: Banyak pasangan segitiga yang kongruen ada 2 pasang, yaitu         Jawaban: B Contoh 2: Soal UN Matematika SMP/MTS...
Baca selengkapnya

Trigonometri

Gambar
Fungsi Trigonometri dan Sudut Istimewa pada Trigonometri By atikroest Halo, squad...! Selamat datang kembali di official page nya atikroest.blogspot.com. Tempat di mana squad dapat belajar kapan saja, dan di mana saja. Kali ini, akan membahas mengenai fungsi trigonometri dan sudut istimewa pada trigonometri. Trigonometri adalah cabang ilmu matematika yang mempelajari sudut dalam segitiga dan fungsi trigonometri. Perbandingan trigonometri terdiri atas fungsi sinus, cosinus, tangen, dan fungsi kebalikan dari ketiga fungsi tersebut. Definisi Sudut dan Ukuran Sudut Sudut adalah suatu bangun yang dibentuk oleh suatu titik pangkal tertentu dan dua sinar dengan titik pangkal yang sama. Tempat titik pangkal yang merupakan pertemuan dua sinar disebut  titik sudut . Sedangkan dua sinar tersebut dinamakan  kaki sudut . Untuk lebih jelasnya perhatikan gambar berikut. Perbandingan Trigonometri Perbandingan trigonometri meliputi fungsi sinus, cosinus, tangen...
Baca selengkapnya

Bangun datar

Gambar
Ciri-ciri dan Sifat Bangun Datar   Bangun datar adalah suatu bentuk dua dimensi dari bangun-bangun yang mempunyai permukaan datar pada luas, panjang, lebar, dan kelilingnya. Macam-macam bangun datar, antara lain persegi, persegi panjang, lingkaran, segitiga, jajar genjang, belah ketupat, layang-layang, trapesium, segi lima atau pentagon, dan segi enam atau hexagon. Kamu juga bisa membaca salah satu rekomendasi buku berikut ini jika ingin mengetahui lebih luas lagi tentang bangun datar yang belum kamu ketahui. Berikut ini adalah beberapa ciri-ciri dan sifat bangun datar, antara lain sebagai berikut: 1. Persegi Persegi adalah bangun datar dua dimensi yang memiliki bentuk pada keempat rusuk yang sisinya sama panjang dan memiliki empat sudut siku-siku sebesar 90 derajat. Perhatikan contoh gambar di bawah ini. Ciri-ciri dan sifat bangun datar persegi, antara lain: Memiliki sisi-sisi yang sama panjang. Memiliki dua diagonal yang sama panjang (keduanya saling berpotongan dan membentuk teg...
Baca selengkapnya