Trigonometri
Fungsi Trigonometri dan Sudut Istimewa pada Trigonometri

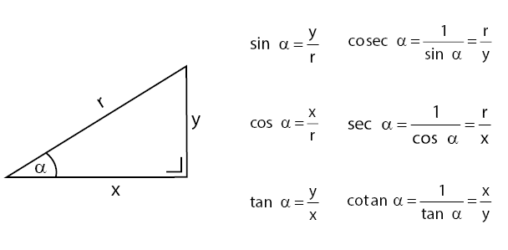
Cara untuk mengingat perbandingan trigonometri dapat dilakukan dengan Jembatan Keledai: SinDeMi CosSaMi TanDeSa.
Perhatikan gambar segitiga berikut!
Nilai sudut istimewa dalam radian :
:
Halo, squad...! Selamat datang kembali di official page nya atikroest.blogspot.com. Tempat di mana squad dapat belajar kapan saja, dan di mana saja. Kali ini, akan membahas mengenai fungsi trigonometri dan sudut istimewa pada trigonometri. Trigonometri adalah cabang ilmu matematika yang mempelajari sudut dalam segitiga dan fungsi trigonometri. Perbandingan trigonometri terdiri atas fungsi sinus, cosinus, tangen, dan fungsi kebalikan dari ketiga fungsi tersebut.
Definisi Sudut dan Ukuran Sudut
Sudut adalah suatu bangun yang dibentuk oleh suatu titik pangkal tertentu dan dua sinar dengan titik pangkal yang sama. Tempat titik pangkal yang merupakan pertemuan dua sinar disebut titik sudut. Sedangkan dua sinar tersebut dinamakan kaki sudut. Untuk lebih jelasnya perhatikan gambar berikut.

Perbandingan Trigonometri
Perbandingan trigonometri meliputi fungsi sinus, cosinus, tangen, dan fungsi kebalikan dari ketiga fungsi tersebut. Perbandingan trigonometri dapat dilihat seperti penjelasan di bawah.

Cara untuk mengingat perbandingan trigonometri dapat dilakukan dengan Jembatan Keledai: SinDeMi CosSaMi TanDeSa.
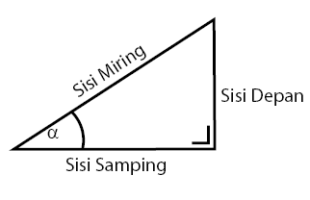
Perhatikan gambar segitiga berikut!

- SinDeMi: Sinus Depan Miring
- CosSaMi: Cosinus Samping Miring
- TanDeSa: Tangen Depan Samping
Sudut Istimewa pada Trigonometri
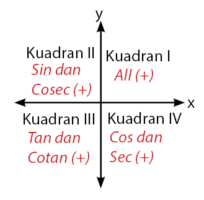
Sebelum membahas mengenai sudut istimewa pada trigonometri dan nilainya, perhatikan dulu pembagian daerah diagram kartesius berikut.

Pembagian diagram kartesius dalam empat kuadran dapat mempermudah squad untuk menentukan nilai perbandingan trigonometri. Pada kuadran I semua nilai (sin, cos, tan, dan kebalikannya) bernilai positif. Perbndingan trigonometri pada kuadran II yang bernilai positif hanya sin dan kebalikannya (cosec). Pada kuadran III, perbandngan trigonometri yang bernilai postif hanya tan dan kebalikannya (cotan). Sedangkan pada kuadran IV, perbndingan trigonometri yang bernilai positif hanya cos dan sec. Squad hanya perlu menghafal nilai fungsi sinus untuk sudut istimewa  ,
,  ,
,  , dan
, dan  . Nilai sudut istimewa lainnya akan mengikuti sesuai rumus pada fungsi identitas trigonometri yang akan diberikan di bawah :
. Nilai sudut istimewa lainnya akan mengikuti sesuai rumus pada fungsi identitas trigonometri yang akan diberikan di bawah :
Rumus trigonometri sudut berelasi :
Sudut
Sudut
Sudut 
Sudut 
Sudut 
Sudut 
Sudut 
Sudut 
Sudut 
Cari nilai dari cos  !
!
Pembahasan:
Pilih salah satu rumus fungsi identitas trigonometri!
Misalkan pilih
Pembahasan:
Pilih salah satu rumus fungsi identitas trigonometri!
Misalkan pilih
Selanjutnya,
Sudut  berada pada kuadran IV. Fungsi cosinus pada kuadran IV adalah positif. Nilai
berada pada kuadran IV. Fungsi cosinus pada kuadran IV adalah positif. Nilai  . Hal ini sesuai dengan pernyataan sebelumnya, bukan?
. Hal ini sesuai dengan pernyataan sebelumnya, bukan?
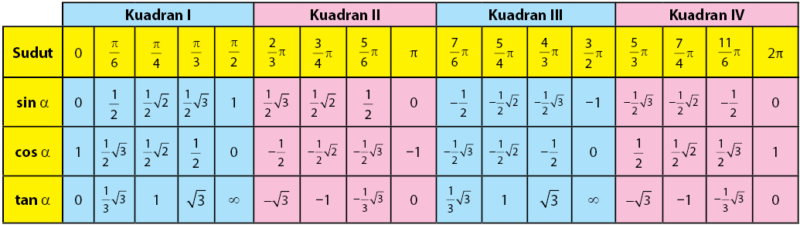
Berikut ini adalah tabel nilai fungsi trigonometri untuk sudut-sudut istimewa
Nilai sudut istimewa dalam derajat:


Nilai sudut istimewa dalam radian

Cara menghafal nilai sudut istimewa pada fungsi sinus atau cosinus juga dapat dilakukan dengan menggunakan grafik fungsi sinus dan grafik fungsi cosinus. Sedangkan untuk memperoleh nilai tangen dari sudut istimewa dapat menggunakan rumus berikut.
Koordinat Katesius dan koordinat kutub



Pengertian Koordinat Kartesius
Koordinat Kartesius adalah letak suatu titik pada bidang yang dinyatakan dalam absis (x) dan ordinat (y). Pada koordinat kartesius letak suatu titik P dinyatakan dengan himpunan pasangan terurut P(x,y)
Koordinat x sebagai absis, yaitu jarak titik ke sumbu Y.
Koordinat y sebagai ordinat, yaitu jarak titik ke sumbu X.
Koordinat x sebagai absis, yaitu jarak titik ke sumbu Y.
Koordinat y sebagai ordinat, yaitu jarak titik ke sumbu X.
Pengertian Koordinat Kutub (Polar)
Koordinat Polar atau koordinat kutub adalah letak suatu titik pada bidang yang dinyatakan dalam bentuk jarak (r) dan sudut (α).
Pada koordinat kutub, letak suatu titik P dinyatakan dengan dua ukuran, yaitu jarak r dan ukuran sudut α.
Hubungan antara Koordinat Kartesius dan Koordinat Kutub (Polar)
Jarak r adalah jarak titik P ( x, y) ke titik asal O (0,0). Jarak r diperoleh dengan rumus:
Sudut α adalah sudut antara sumbu X positif dengan garis penghubung titik P dengan titik asal O (0,0) yang dihitung berlawanan arah dengan arah jarum jam.
Koordinat kutub titik P dinyatakan dengan P (r, α)
Jika digambarkan, grafik koordinat kartesius dan grafik koordinat polar sebagai berikut
Pada Koordinat polar atau kutub dengan titik pusat O, posisi titik (objek) P dinyatakan dengan (r, α), dimana r adalah jarak OP dan α adalah sudut antara OP dengan sumbu OX positif.
Besar sudut α dihitung mulai dari sumbu OX positif berputar berlawanan arah dengan arah perputaran jarum jam
Perbedaan dan Persamaan antara Koordinat Kartesius dan Koordinat Polar.
Koordinat Kartesius
Pada koordinat kartesius letak suatu titik P dinyatakan dengan himpunan pasangan terurut P(x,y)
→ Koordinat x sebagai absis, yaitu jarak titik ke sumbu Y.
→ Koordinat y sebagai ordinat, yaitu jarak titik ke sumbu X.
→ Koordinat x sebagai absis, yaitu jarak titik ke sumbu Y.
→ Koordinat y sebagai ordinat, yaitu jarak titik ke sumbu X.
Koordinat Kutub (Polar)
Pada koordinat kutub, letak suatu titik P dinyatakan dengan dua ukuran, yaitu jarak r dan ukuran sudut α.
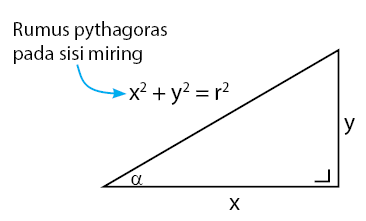
→ Jarak r adalah jarak titik P ( x, y) ke titik asal O (0,0). Jarak r diperoleh dengan rumus pythagoras:
→ Jarak r adalah jarak titik P ( x, y) ke titik asal O (0,0). Jarak r diperoleh dengan rumus pythagoras:
→ Sudut α adalah sudut antara sumbu X positif dengan garis penghubung titik P dengan titik asal O (0,0) yang dihitung berlawanan arah dengan arah jarum jam.
→ Koordinat kutub titik P dinyatakan dengan P (r, α).
→ Koordinat kutub titik P dinyatakan dengan P (r, α).
Contoh Soal dan Pembahasannya
A. Mengubah atau Mengkonversi Koordinat Polar ke Koordinat Kartesius
Soal 1.
Koordinat kartesius dari titik (10, 315°) adalah ….
A. (-5, -5√2)
B. (-5, 5√2)
C. (5√2, 5√2)
D. (5√2, -5√2)
E. (5, -5√2)
A. (-5, -5√2)
B. (-5, 5√2)
C. (5√2, 5√2)
D. (5√2, -5√2)
E. (5, -5√2)
Jawab : D
» Sudut 315° (kuadran IV) —–> (x, -y)
» Dari pilihan jawaban di atas maka kemungkinan jawabannya D atau E
» (r, α) ——> (10, 315°)
» Dari pilihan jawaban di atas maka kemungkinan jawabannya D atau E
» (r, α) ——> (10, 315°)
x = 10 . cos 315°
x = 10 . ½√2
x = 5√2
x = 10 . ½√2
x = 5√2
y = 10 . sin 315°
y = 10 . -½√2
y = -5√2
Jadi koordinat kartesiusnya adalah (5√2, -5√2)
y = 10 . -½√2
y = -5√2
Jadi koordinat kartesiusnya adalah (5√2, -5√2)
Untuk lebih jelas dapat dilihat pada gambar di samping.
B. Mengubah atau Mengkonversi Koordinat Kartesius ke Koordinat Polar
Soal 2.
Koordinat kutup dari titik (-6, 6√3) adalah ….
A. (12, 30°)
B. (12, 60°)
C. (12, 90°)
D. (12, 120°)
E. (12, 210°)
A. (12, 30°)
B. (12, 60°)
C. (12, 90°)
D. (12, 120°)
E. (12, 210°)
Jawab : D
Cara biasa
r² = (-6)² + (6√3)²
r² = 36 + 108
r² = 144
r = 12
Cara biasa
r² = (-6)² + (6√3)²
r² = 36 + 108
r² = 144
r = 12
a = arc tan (6√3) / -6
a = arc tan -√3
a = 120°
Jadi koordinat kutubnya adalah (12, 120°)
a = arc tan -√3
a = 120°
Jadi koordinat kutubnya adalah (12, 120°)
Cara praktis
» (-6, 6√3) ——-> (-x, y) —–> maka berada di kuadran II
» Dari pilihan jawaban di atas yang berada di kuadran II yaitu hanya pilihan D
» Sedangkan r tidak usah dicari karena dari pilihan jawaban semuanya sama
» (-6, 6√3) ——-> (-x, y) —–> maka berada di kuadran II
» Dari pilihan jawaban di atas yang berada di kuadran II yaitu hanya pilihan D
» Sedangkan r tidak usah dicari karena dari pilihan jawaban semuanya sama
Identitas Trigonometri
Identitas trigonometri adalah bentuk persamaan trigonometri yang menghubungkan suatu perbandingan trigonometri dengan perbandingan trigonometri yang lainnya.

Dalam hal ini terdapat identitas trigonometri dasar yang sudah pernah dibahas pada materi sebelumnya, yaitu :

Sedangkan dari rumus perbandingan tangens diperoleh :
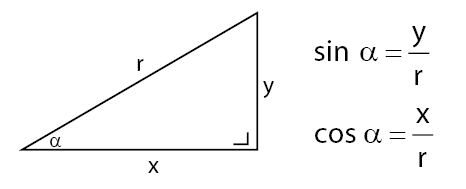
Untuk lebih jelasnya, ikutilah contoh soal berikut ini :
01. Buktikanlah bahwa 3 + 5sin2 α = 8 – 5cos2 α
Jawab
Ruas kiri = 3 + 5sin2 α
= 3 + 5(1 – cos2 α )
= 3 + 5 – 5cos2 α
= 8 – 5cos2 α
= Ruas kanan
02. Buktikanlah bahwa sec2 α – sin2 α .sec2 α = 1
Jawab
Disamping itu terdapat pula identitas-identitas dasar yang lain, yang didapat dari proses sebagai berikut:

Sedangkan dari rumus perbandingan tangens diperoleh :
Sebenarnya, ada banyak fungsi identitas trigonometri. Tiga fungsi identitas trigonometri yang diberikan di atas hanyalah sebagian. Rumus tersebut merupakan rumus turunan yang diperoleh dengan menghubungkan satu fungsi trigonometri dengan fungsi trigonometri lainnya. Karena merupakan fungsi identitas, fungsi-fungsi tersebut dapat dibuktikan kebenarannya. Cara membuktikannya dapat dengan cara merubah ruas kiri agar sama dengan ruas kanan, ataupun sebaliknya.
Sebagai contoh, akan dibuktikan kebenaran dari rumus identitas trigonometri  .
.
Pembuktian rumus 
Perhatikan gambar di bawah!
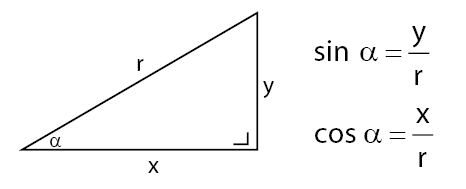
Sebelum melanjutkan pembuktian rumus, ingat kembali persamaan pada pythagoras seperti yang terlihat pada gambar di bawah.

Substitusi persamaan  ke dalam persamaan terakhir yang diperoleh, sehingga menjadi seperti berikut.
ke dalam persamaan terakhir yang diperoleh, sehingga menjadi seperti berikut.
Terbukti
Untuk pembuktian rumus identitas lainnya dapat dibuktikan dengan teknik dan melibatkan persamaan  yang telah dibuktikan sebelumnya.
yang telah dibuktikan sebelumnya.
Selain identitas dasar di atas, identitas-identitas yang lain dapat dikembangkan dengan memanfaatkan rumus identitas dasar tersebut.Untuk lebih jelasnya, ikutilah contoh soal berikut ini :
01. Buktikanlah bahwa 3 + 5sin2 α = 8 – 5cos2 α
Jawab
Ruas kiri = 3 + 5sin2 α
= 3 + 5 – 5cos2 α
= 8 – 5cos2 α
= Ruas kanan
02. Buktikanlah bahwa sec2 α – sin2 α .sec2 α = 1
Jawab
Selanjutnya, akan diulas identitas trigonometri lain yang tidak kalah penting dengan rumus identitas trigonometri yang sudah diberikan sebelumnya. Selain rumus identitas di atas, terdapat rumus identitas lain yaitu rumus identitas trigonometri dari rumus sudut rangkap fungsi trigonometri. Perhatikan persamaan di bawah.

Fungi identitas trigonometri yang diberikan di atas dapat digunakan untuk membantu menyelesaikan soal limit fungsi trigonometri atau berbagai topik masalah dalam pembahasan matematika lain. Untuk menambah pemahaman sobat idschool tentang rumus identitas trigonometri, simak contoh soal dan pembahasan tentang pembuktian identitas trigonometri di bawah.
Contoh Soal dan Pembahasan
Buktikan bahwa persamaan identitas trigonometri di bawah adalah benar!
Bukti:
Terbukti
Aturan cosinus dan Sinus

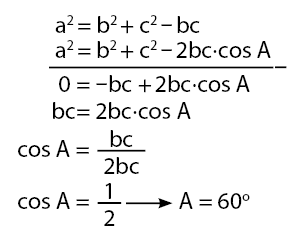
Aturan cosinus dan Sinus
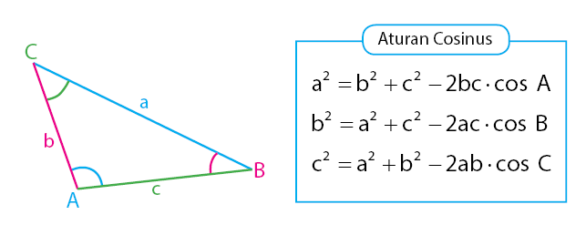
Aturan Cosinus
Sudah disinggung sedikit sebelumnya, bahwa aturan cosinus dapat digunakan untuk menentukan panjang salah satu sisi segitiga atau besar salah satu sudut segitiga. Persamaan yang terdapat pada aturan cosinus juga diperoleh dengan memanfaatkan fungsi trigonometri dan teorema pythagoras.
Sebagai pengantar, simak cara mendapatkan tiga persamaan pada aturan cosinus di bawah.
Perhatikan gambar di bawah!

Pada  :
:
Pada  dapat diperoleh persamaan di bawah (berdasar teorema pythagoras):
dapat diperoleh persamaan di bawah (berdasar teorema pythagoras):
Persamaan akhir yang di atas merupakan salah satu aturan cosinus. Dengan mengikuti langkah serupa seperti yang telah dikerjakan di atas, akan diperoleh tiga buah persamaan aturan cosuinus. Tiga buah persamaan tersebut dapat dilihat pada gambar di bawah.

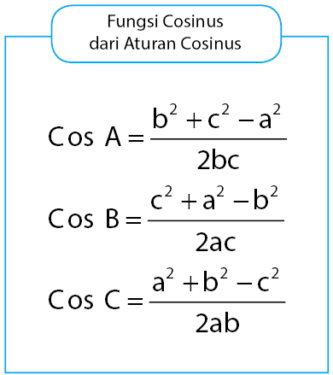
Berdasarkan tiga persamaan aturan cosinus di atas, dapat diperoleh rumus fungsi cosinus yang dapat digunakan untuk menentukan besar sudut segitiga jika diketahui panjang ketiga sisi segitiga. Persamaan fungsi cosinus tersebut dapat dilihat pada persamaan di bawah.

Contoh Soal dan Pembahasan
Pada suatu segitiga dengan sisi-sisi a, b, dan c memenuhi  . Maka besar sudut A adalah ….
. Maka besar sudut A adalah ….
A.
B.
C.
D.
E.
A.
B.
C.
D.
E.
Pembahasan:
Diketahui:
Sehingga,
Salah satu rumus cosinus adalah:
Berdasarkan dua persamaan di atas, akan diperoleh nilai cos A.
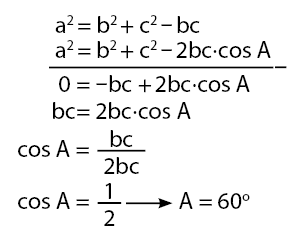
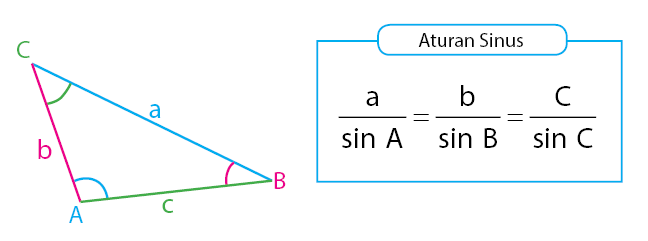
Aturan Sinus
Aturan sinus merupakan persamaan yang menyatakan hubungan tiga sudut dan tiga sisi yang terdapat pada segitiga sembarang. Tujuan dari penggunaan aturan sinus adalah untuk mengetahui panjang sisi segitiga yang terdapat pada segitiga sembarang. Atau dapat juga digunakan untuk mengetahui besar sudut segitiga yang belum diketahui.
Sebelumnya, squad sepertinya perlu tahu dari mana persamaan sinus diperoleh. Simak cara mendapatkan persamaan aturan sinus yang akan diberikan di bawah.
Perhatikan gambar di bawah!

Pada  :
:
Pada  :
:
Berdasarkan dua persamaan di atas, dapat disimpulkan bahwa
Dengan cara yang serupa akan diperoleh persamaan aturan sinus seperti yang diberikan pada persamaan di bawah.

Fungsi aturan sinus di atas dapat digunakan untuk menentukan panjang sisi segitiga yang belum diketahui. Selain itu, juga dapat digunakan untuk mencari besar sudut segitiga yang belum diketahui.
Untuk menambah pemahaman squad, akan diberikan contoh soal yang dilengkapi dengan pembahasan mengenai penggunaan aturan sinus untuk menentukan panjang salah satu sisi segi tiga yang belum diketahui. Simak contoh soal dan pembahasan aturan sinus yang diberikan di bawah.
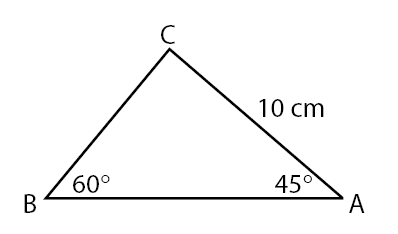
Contoh Soal dan Pembahasan
Suatu segitiga ABC memiliki panjang AC = 8 cm. Jika besar  dan
dan  , maka panjang BC = … cm.
, maka panjang BC = … cm.
Pembahasan:
Berdasarkan informasi yang diberikan pada soal, dapat diperoleh informasi seperti berikut ini.

Panjang BC dapat dicari menggunakan aturan sinus.
Jawaban: E
Oke, sekian dulu pembahasan mengenai fungsi trigonometri dan sudut istimewa pada trigonometri. Jangan lupa baca juga pembahasan materi lainnya biar squad semakin pandai bisa jadi yang terbaik. Semoga bermanfaat.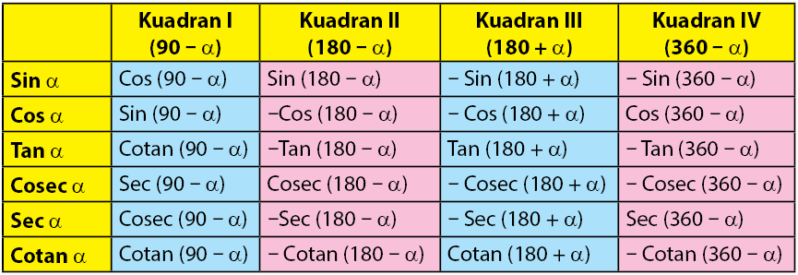
![[Tags] c3 Pengertian Koordinat Kartesius dan Polar Dalam Matematika](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEikx191nltJPonIjXzxSO1gIptE0QIfwsSs091-qLxEQG6XlRlX3C5h9BqWbJ9Xzkz9OXMn1g4lyICdfediBMm-3NsnmFxmjcnI1wY9gpMxn4LTKj6YdZnh1taQ8Kg2bsMd40rCj0x2fccH/s1600/Capture61.PNG)
![[Tags] c3 Pengertian Koordinat Kartesius dan Polar Dalam Matematika](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh1mV4o2XWt3VILIUbx-H0zrPPgdBv7h1-BYB6nKOYB9IhhZp_KUHqxgIBAELQmkcawid_NlxqcX9z8FiShge-WnhgXzqhwxkameSeaPhTyw_r7d2WSPOXz-WwTudxqG49LdLe5xnfV_dBl/s1600/Capture62.PNG)





Wawww
BalasHapusMasuk
BalasHapusYou wlkk
BalasHapusOke woo
BalasHapus