Himpunan

Himpunan dan Diagram Venn

Halo Squad! Kamu pernah tidak ikut suatu perkumpulan di sekolahmu? Di sekolah biasanya terdapat banyak sekali suatu perkumpulan seperti perkumpulan murid-murid yang hobi basket, sepak bola, bulu tangkis, tennis, melukis, menari, hingga perkumpulan murid-murid yang suka matematika. Nah dari macam-macam perkumpulan tersebut pernah dengar tidak dengan istilah Himpunan Siswa Gemar Melukis? Yapjadi perkumpulan-perkumpulan yang tadi telah disebutkan juga bisa dibilang Himpunan. Dengan adanya himpunan, kita bisa mengetahui dan membedakan apa saja yang termasuk dalam himpunan atau tidak. Yuk kita belajar lebih lanjut tentang himpunan!
himpunan
Visualisasi himpunan


Contoh Himpunan:
  1. Himpunan hewan karnivora
  2. Himpunan warna pelangi
  3. Himpunan bilangan asli
  4. Himpunan bilangan prima antara 10 dan 40
Contoh Bukan Himpunan:
  1. Himpunan lukisan yang menarik ( karena arti kata menarik berbeda-beda menurut setiap orang)
  2. Himpunan orang pintar (karena tidak ada ukuran pasti untuk mengukur kepintaran seseorang)
  3. Himpunan warna yang bagus ( karena arti kata bagus berbeda-beda menurut setiap orang)
Squad! Misalnya kamu sudah tahu nihbahwa himpunan bilangan-bilangan prima antara 10 dan 40 adalah 11, 13, 17, 19, 23, 29, 31, 37. Lalu, bagaimana ya caranya menyatakan suatu himpunan? Ternyata ada berbagai cara untuk menuliskan atau menyatakan himpunan-himpunan tersebut. Himpunan dapat dinyatakan dalam 3 bentuk yaitu dengan kata-kata, dengan notasi pembentuk himpunan, dan dengan mendaftarkan anggota-anggotanya.
Aturan Cara Penulisan:
•Penamaan sebuah himpunan dilambangkan dengan huruf kapital (A, B, C,…., Z)
•Penulisan anggota himpunan harus di dalam kurung kurawal {}
•Untuk memisahkan satu anggota dengan anggota lainnya pakai tanda koma (,).
•Jika anggota himpunan masih banyak dan tidak dapat disebutkan satu per satu (masih berlanjut) dapat digunakan tanda titik-titik (….)
•Notasi ϵ dibaca “anggota dari”
•Notasi ∉ dibaca “bukan anggota dari
Sebelum mempelajari lebih lanjut tentang materi himpunan, kamu harus tahu terlebih dahulu istilah-istilah penting yang ada dalam himpunan. Apa saja ya istilah-istilah penting yang ada di Himpunan.
1. Kardinalitas
Pertama adalah Kardinalitas . Kardinalitas adalah banyaknya anggota himpunan yang berbeda. Nah untuk menyatakan banyaknya anggota yang berbeda dalam suatu himpunan menggunakan notasi n. Contohnya adalah tentukan banyaknya anggota himpunan A= { Huruf pembentuk kata “cermat’ } . Berarti kamu menjawabnya dengan cara n(A) = 6.
2. Himpunan Semesta
Himpunan Semesta (Sumber: MarchSchilder.com)
Himpunan semesta adalah himpunan yang memuat semua anggota atau objek himpunan yang dibicarakan dan dilambangkan dengan S. Di dalam himmpunan semesta, terdapat beberapa anggota. 
3. Himpunan Kosong
Himpunan kosong artinya himpunan yang tidak mempunyai anggota. Himpunan kosong ditulis dengan notasi atau simbol { } atau ∅. Contohnya yaitu jika kamu disuruh untuk menyebutkan nama hari yang berawalan dari huruf z, tetapi tidak ada jawabannya karena tidak ada hari yang berawalan huruf z. Berati itu termasuk himpunan kosong. Dijawab seperti ini yaa: n(E) = { } atau n(E) = ∅. Tapi ingat ya Squad, jangan menuliskan himpunan kosong dengan cara n(E) = {0}. Ini salah ya! Ini karena {0} mempunyai anggota yaitu 0, bukan himpunan kosong.
pengertian dan istilah himpunanHimpunan Kosong (sumber: MarchSchilder.com)

Materi himpunan dan diagram venn memiliki keterkaitan yang erat. Himpunan menyatakan anggota yang tergabung dalam sebuah syarat tertentu. Sedangkan diagram venn menggambarkan himpunan tersebut dalam sebuah diagram agar lebih mudah dipahami.
Contoh:
Himpunan bilangan Asli
Anggota: {1, 2, 3, 4, 5, 6, 7, …}
Himpunan bilangan prima kurang dari 13
Anggota:{2, 3, 5, 7, 11}
Hubungan himpunan dan diagram venn dapat dilihat pada gambar di bawah.
Himpunan
A = himpunan bilangan ganjil < 15 A = {1, 3, 5, 7, 9, 11, 13}   B = himpunan bilangan kelipatan tiga yang kurang dari 17 B = {3, 6, 9, 12, 15}

Diagram Venn
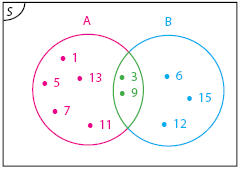
Himpunan dan Diagram Venn

Himpunan

Himpunan merupakan kumpulan benda atau objek yang didefinisikan dengan jelas. Lambang untuk menyimbolkan himpunan adalah huruf besar, misal A, B, C, dan lain sebagainya. Untuk menyatakan anggota dari sebuah himpunan adalah \in. Sedangkan untuk menyatakan anggota yang tidak termasuk dalam sebuah himpunan adalah \notin. Untuk menyatakan banyaknya anggota suatu himpunan A dinotasikan dengan n(A).
Contoh:
Himpunan A = {1, 2, 3, 4, 5, 6, 7, 8, 9}.
Banyak anggota himpunan A = n(A) = 9
Himpunan memiliki anggota yang terhingga atau tak terhingga. Himpunan dengan banyak anggota terhingga atau dibatasi samoai batas tertentu disebut himpunan berhingga. Sedangkan, himpunan dengan banyak anggota tak terbatas adalah himpunan tak berhingga.
Contoh:
Himpunan berhingga: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Himpunan tak berhingga: {25, 27, 29, 31, …}
Himpunan dapat dinyatakan dalam salah satu cara di bawah.
Menyebutkan semua anggotanya
Contoh: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; {25, 27, 29, 31, …}; dan lain sebagainya.
Menuliskan sifat anggotanya
Contoh: himpunan bilangan asli kurang dari 10, himpunan bilangan ganjil lebih dari 23, dan lain sebagainya.
Notasi pembentuk himpunan
Contoh: {x | x < 10, x \in bilangan asli}, {x | x > 23, x \inbilangan ganjil}, dan lain sebagainya.
Macam-Macam Himpunan
Himpunan Semesta
Himpunan semesta adalah himpunan yang memuat semua anggota himpunan. Notasi untuk himpunan semesta adalah S.
Himpunan Bagian
A merupakan himpunan bagian B jika setiap anggota himpunan A merupakan anggota himpunan B. Notasi untuk menyatakan himpunan bagian adalah C. Simbol untuk menyatakan A himpunan bagian B adalah . Himpunan kosong merupakan himpunan bagian dari setiap himpunan. Setiap himpunan merupakan himpunan bagian dari himpunan itu sendiri.
Rumus mencari banyaknya himpunan bagian.
Himpunan = A
Banyak anggota himpunan A = n(A)
Banyaknya himpunan bagian A adalah 2^{n(A)}
Contoh:
B = {1, 2, 3}
n(B) = 3
Banyaknya himpunan bagian B adalah 2^{3} = 8 yaitu { }; {1}; {2}; {3}; {1, 2}; {1, 3}; {2, 3}; {1, 2, 3}.
Himpunan Kosong
Himpunan kosong adalah himpunan yang tidak mempunyai anggota. Himpunan kosong akan selalu menjadi himpunan bagian dari anggota himpunan bagian. Notasi himpunan kosong adalah { } atau .

pengertian dan istilah himpunan

Hubungan Antarhimpunan

Pembahasan selanjutnya dalam materi himpunan dan diagram venn adalah hubungan antarhimpunan. Hubungan antarhimpunan meliputi irisan, gabungan, komplemen himpunan, dan selisih himpunan. Lebih lanjut mengenai keempatnya dapat dilihat seperti pembahasan di bawah.
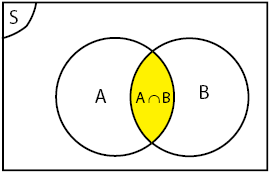
Irisan
Irisan dua himpunan A dan B adalah himpunan yang anggota-anggotanya merupakan anggota A dan anggota B.
  \[A \cap B = \left \{ x \mid x \in A dan x \in B \right \} \]
Irisan
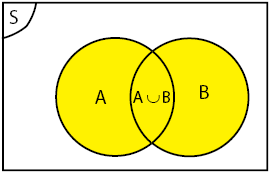
Gabungan
Gabungan dua himpunan A dan B adalah himpunan yang anggota-anggotanya merupakan anggota himpunan A atau anggota himpunan B.
  \[ A \cup B = \left \{ x \mid x \in A atau x \in B \right \} \]
Gabungan
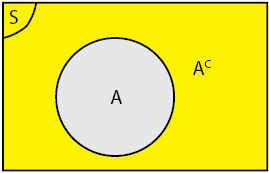
Komplemen
A^{C} adalah himpunan yang anggota-anggotanya merupakan anggota himpunan semesta namun bukan anggota himpunan A.
  \[A^{C} = \left \{ x \mid x \in S dan x \notin A\right \} \]
Komplemen

Selisih
A − B adalah himpunan yang anggota-anggotanya merupakan anggota himpunan A namun bukan anggota himpunan B.
  \[A - B = A \cap B^{C} \]
Selisih

Sifat-Sifat Operasi Himpunan

Pembahasan dalam materi himpunan dan diagram venn yang tidak kalah penting untuk dibahasa adalah sifa-sifat operasi pada himpunan. Sifat-sifat operasi himpunan meliputi komutatif, asosiatif, ditributif, dan dalil de Morgan.

Komutatif
  \[A \cap B = B \cap A \]
  \[A \cup B = B \cup A \]

Asosiatif
  \[\left(A \cap B \right) \cap C = A \cap \left( B \cap C \right) \]
  \[\left(A \cup B \right) \cup C = A \cup \left( B \cup C \right) \]
Distributif
  \[A \cap \left( B \cup C \right) = \left( A \cap B \right) \cup \left( A \cap C \right) \]
  \[A \cup \left( B \cap C \right) = \left( A \cup B \right) \cap \left( A \cup C \right) \]
Dalil de Morgan
  \[\left( A \cap B \right)^{C} = A^{C} \cup B^{C} \]
  \[\left( A \cup B \right)^{C} = A^{C} \cap B^{C} \]

Contoh Soal dan Pembahasan

Kelas VII-A terdiri dari 31 siswa. Terdapat 15 siswa mengikuti kompetisi Matematika, 13 siswa mengikuti kedua kompetisi IPA, dan 7 siswa tidak mengikuti kompetisi tersebut. Banyak siswa yang mengikuti kedua kompetisi tersebut adalah ….
A.       28 siswa
B.       8 siswa
C.       5 siswa
D.       4 siswa
SOAL UN Matematika SMP 2016
Pembahasan:
Misalkan: x = banyak siswa yang mengikuti kedua kompetisi.
Himpunan tersebut dapat digambarkan dalam bentuk diagram venn seperti gambar di bawah.
Contoh soal dan pembahasan matematika smp himpunan

Semua siswa = 31
  \[x + 15 - x + 13 - x + 7 = 31\]
  \[35 - x = 31\]
  \[x = 4\]
Jadi, banyak siswa yang mengikuti kedua kompetisi tersebut adalah 4 siswa.
Jawaban: D
Demikianlah tadi ulasan materi tentang himpunan dan diagram venn. Meliputi sifat-sifat himpunan, dan contoh soal himpunan dan diagram venn berserta dengan pembahasannya. Terimakasih sudah mengunjungi atikroest.blogspot, semoga bermanfaat.

Komentar

Posting Komentar

Postingan populer dari blog ini

Kesebangunan dan Kekongruenan (soal dan pembahasan)

Gambar
Kesebangunan dan Kekongruenan Hallo sobat atikroest, pada halaman ini akan mengupas tentang contoh soal kesebangunan dan kekongruenan. Seperti kisi-kisi yang telah dikeluarkan BSNP, materi kesebangunan dan kekongruenan akan kembali muncul di ujian nasional. Kisi-kisi untuk kesebangunan dan kekongruenan diberikan dalam 3 (tiga) level kognitif, yaitu pengetahuan dan pemahaman, aplikasi, dan penalaran. Halaman ini akan membahas kisi-kisi UN 2019 dengan materi kesebangunan dan kekongruenan untuk level pengetahuan dan pemahaman. Simak kumpulan soal UN dengan materi kesebangunan dan kekongruenan pada pembahasan di bawah. BAGIAN I Contoh 1: Soal UN Matematika SMP/MTS Tahun 2014 Perhatikan gambar! Banyak pasangan segitiga yang kongruen adalah …. A.     1 B.     2 C.     3 D.     4 Pembahasan: Banyak pasangan segitiga yang kongruen ada 2 pasang, yaitu         Jawaban: B Contoh 2: Soal UN Matematika SMP/MTS...
Baca selengkapnya

Trigonometri

Gambar
Fungsi Trigonometri dan Sudut Istimewa pada Trigonometri By atikroest Halo, squad...! Selamat datang kembali di official page nya atikroest.blogspot.com. Tempat di mana squad dapat belajar kapan saja, dan di mana saja. Kali ini, akan membahas mengenai fungsi trigonometri dan sudut istimewa pada trigonometri. Trigonometri adalah cabang ilmu matematika yang mempelajari sudut dalam segitiga dan fungsi trigonometri. Perbandingan trigonometri terdiri atas fungsi sinus, cosinus, tangen, dan fungsi kebalikan dari ketiga fungsi tersebut. Definisi Sudut dan Ukuran Sudut Sudut adalah suatu bangun yang dibentuk oleh suatu titik pangkal tertentu dan dua sinar dengan titik pangkal yang sama. Tempat titik pangkal yang merupakan pertemuan dua sinar disebut  titik sudut . Sedangkan dua sinar tersebut dinamakan  kaki sudut . Untuk lebih jelasnya perhatikan gambar berikut. Perbandingan Trigonometri Perbandingan trigonometri meliputi fungsi sinus, cosinus, tangen...
Baca selengkapnya

Bangun datar

Gambar
Ciri-ciri dan Sifat Bangun Datar   Bangun datar adalah suatu bentuk dua dimensi dari bangun-bangun yang mempunyai permukaan datar pada luas, panjang, lebar, dan kelilingnya. Macam-macam bangun datar, antara lain persegi, persegi panjang, lingkaran, segitiga, jajar genjang, belah ketupat, layang-layang, trapesium, segi lima atau pentagon, dan segi enam atau hexagon. Kamu juga bisa membaca salah satu rekomendasi buku berikut ini jika ingin mengetahui lebih luas lagi tentang bangun datar yang belum kamu ketahui. Berikut ini adalah beberapa ciri-ciri dan sifat bangun datar, antara lain sebagai berikut: 1. Persegi Persegi adalah bangun datar dua dimensi yang memiliki bentuk pada keempat rusuk yang sisinya sama panjang dan memiliki empat sudut siku-siku sebesar 90 derajat. Perhatikan contoh gambar di bawah ini. Ciri-ciri dan sifat bangun datar persegi, antara lain: Memiliki sisi-sisi yang sama panjang. Memiliki dua diagonal yang sama panjang (keduanya saling berpotongan dan membentuk teg...
Baca selengkapnya