Langsung ke konten utama

Bangun ruang sisi datar


Bangun Ruang Sisi Datar

By  | July 26, 2017
Bangun ruang termasuk dalam dimensi tiga. Ukuran yang dimiliki bangun ruang meliputi panjang, lebar, dan tinggi. Bangun datar merupakan bangun dimensi dua. Contoh bangun sisi datar adalah segi empat, persegi panjang, segitiga, trapesium, dan lain sebagainya. Bangun Ruang Sisi Datar dapat digambarkan sebagai bangun ruang yang setiap sisinya disusun oleh bangun datar. Anggota bangun ruang sisi datar meliputi kubus, balok, prisma, dan limas.

Bangun Ruang Sisi Datar 1 – Kubus

Bangun ruang pertama yang akan kita pelajari adalah kubus. Bangun kubus ditunjukkan pada gambar di bawah.

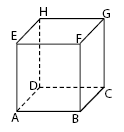
bangun ruang sisi datar
Karakteristik Kubus:
  • Mempunyai 6 sisi yang kongruen berbentuk persegi.
  • Mempunyai 8 titik sudut dan 12 rusuk yang sama panjang.
  • Tersusun atas 6 sisi berbentuk persegi.
  • Kubus ABCD. EFGH mempunyai 4 diagonal ruang yaitu HB, DF, EC, dan AG.
  • Kubus ABCD.EFGH mempunyai 6 bidang diagonal, yaitu HEBC, EFCD, FGDA, HGBA, EGCA, dan HFBD.
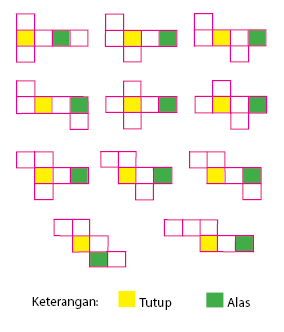
 Jaring – Jaring Kubus:
Bangun ruang kubus dapat dibuat melalui jaring – jaring kubus Kubus dapat dibentuk dari salah satu jaring-jaring di bawah.

jaring-jaring kubus

Rumus pada Kubus
Rumus pada kubus meliputi beberapa persamaan untuk mendapatkan volume kubus dan luas permukaan kubus. Selain itu juga terdapat rumus untuk mendapatkan nilai panjang diagonal sisi dan diagonal ruang secara cepat. Berikut ini adalah beberapa persamaan dalam rumus pada kubus.
Diketahui: panjang rusuk = s
  \[ V_{kubus}= s^{3} \]
  \[ L_{permukaan \; kubus} = 6 \times s^{2} \]
  \[ \textrm{Panjang diagonal sisi} = s \sqrt{2} \]
  \[ \textrm{Panjang diagonal ruang}= s \sqrt{3} \]

Bangun Ruang Sisi Datar 2 – Balok

Bangun ruang sisi datar kedua yang akan dibahas adalah Balok. Gambar balok dapat dilihat seperti gambar di bawah.

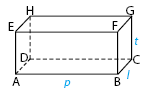
bangun ruang sisi datar
Karakteristik Balok:
  • Terdiri dari 12 rusuk.
  • Mempunyai 8 titik sudut, yaitu A, B, C, D, E, F, G, H.
  • Mempunyai 6 sisi yang berbentuk segi empat.
  • Memiliki 3 pasang segi empat (2 persegi panjang atau persegi pada salah satu sisinya) yaitu ABCD dan EFGH, ABFE dan DCGH, serta BCGF dan ADHE.
  • Balok ABCD.EFGH mempunyai 12 diagonal sisi, yaitu AC, BD, BE, AF, CF, BG, CH, DG, AH, DE, EG, dan FH.
  • Balok ABCD.EFGH mempunyai 4 diagonal ruang yang sama panjang, yaitu HB, DF, CE, dan AG.
  • Balok ABCD.EFGH mempunyai 6 bidang diagonal, yaitu HEBC, EFCD, FGDA, HGBA, EGCA, dan HFBD.
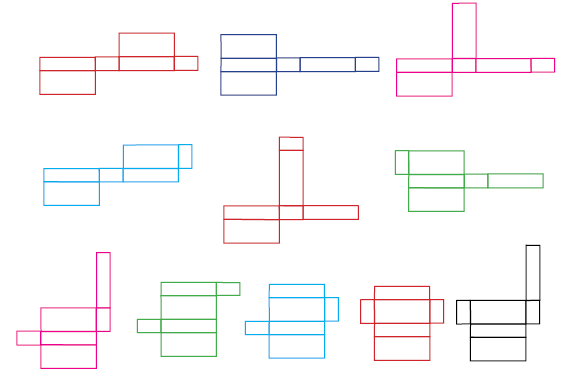
Jaring – jaring Balok:
Variasi jaring-jaring balok dapat dilihat seperti gambar berikut.

jaring-jaring balok

Rumus pada Balok:
Beberapa persamaan dalam rumus pada balok dengan sisi panjang (p), lebar (l), dan tinggi (t) meliputi rumus volume balok dan rumus permukaan balok.
Rumus Volume Balok:
  \[ V_{balok}= p \times l \times t \]
Rumus Luas Permukaan Balok:
  \[ L_{permukaan \; balok} = 2(p \times l) + 2(p \times t) + 2(l \times t) \]
Rumus diagonal ruang pada balok:
  \[ \textrm{diagonal ruang} = \sqrt{p \times l \times t} \]

Bagun Ruang Sisi Datar 3 – Prisma

Ketiga, bangun ruang sisi datar selanjutnya prisma. Gambar prisma dapat dilihat pada gambar di bawah.

bangun ruang sisi datar
Karakteristik Prisma:
  • Mempunyai bidang alas dan bidang atas yang kongruen.
  • Banyak rusuk pada prisma segi n beraturan adalah 3n.
  • Jumlah sisi pada prisma segi n beraturan adalah n + 2.
  • Prisma segi n beraturan memiliki titik sudut sebanyak 2n.
 Jaring – jaring Prisma:

jaring-jaring prisma

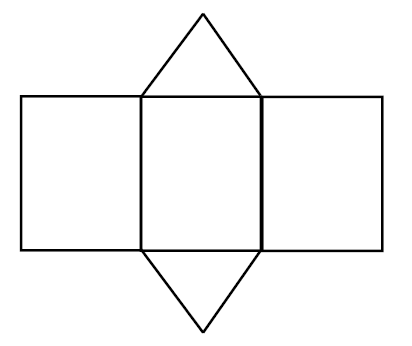
 Rumus pada Prisma:
Luas permukaan prisma:
  \[ \textrm{Luas permukaan prisma} = (2 \times L_{alas}) + K_{alas} \times t_{prisma} \]
Volume prisma:
  \[ \textrm{Volume prisma} = L_{alas} \times t_{prisma} \]

Bagun Ruang Sisi Datar 4 – Limas

Masuk pada bangun ruang sisi datar keempat yang akan dibahas, yaitu bangun ruang dengan sebutan limas. Bangun ruang berbentuk limas memiliki karakteristik seperti yang disebutkan di bawah.
 Karakteristik Limas:
  • Limas adalah bangun ruang tiga dimensi yang dibatasi oleh alas berbentuk segi n dan sisi-sisi tegak berbentuk segitiga.
  • Banyak sisi pada limas segi n adalah n + 1.
  • Banyak rusuk pada limas segi n adalah 2n.
  • Banyak titik sudut pada limas segi n adalah n + 1.
  • Banyak titik sudut pada limas segi n adalah n + 1.
 Jaring – jaring Limas:

jaring-jaring limas

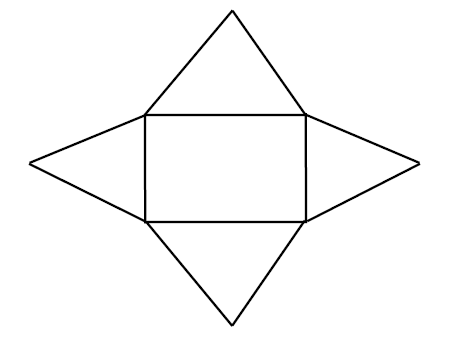
 Rumus pada Limas:
Luas permukaan limas:
  \[ \textrm{Luas permukaan limas} = L_{alas} + \sigma L_{sisi atas} \]
Volume limas:
  \[ V_{limas} = \frac{1}{3} \times L_{alas} \times t_{limas} \]

Contoh Soal dan Pembahasan

Contoh 1 – Soal Bangun Ruang Sisi Datar
Perhatikan gambar berikut!

contoh soal bangun ruang sisi datar

Panjang TU = 10 cm, PQ = 15 cm, QU = 12 cm, dan PS = 9 cm. Luas permukaan prisma tersebut adalah ….(SOAL UN Matematika SMP 2016)
A.       1.500 cm2
B.       1.350 cm2
C.       900 cm2
D.       750 cm2
Pembahasan:
Sisi alas dan atas prisma adalah sisi PQUT dan SRVW. Alas Sisi PQUT dan SRVW merupakan trapesium. Secara lebih jelasnya dapat dilihat pada gambar berikut.

Pembahasan soal bangun ruang sisi datar

Untuk menentukan luas permukaan prisma, kita perlu menghitung sisi TP = WS terlebih dahulu. Sisi TP = WS dapat dihitung menggunakan teorema phytagoras. Perhatikan \Delta PTT'
  \[TP =\sqrt{12^{2}+5^{2}} \]
  \[TP =\sqrt{144 + 25} \]
  \[TP =\sqrt{169} = 13 \; cm\]
Selanjutnya, hitung luas alas prisma dan keliling alas prisma yang merupakan trapesium.

contoh soal bangun ruang sisi datar

  \[K_{trapesium} = 15 + 12 + 10 +13 = 50 \; cm\]
  \[L_{trapesium}=\frac{jumlah sisi sejajar \times t_{trapesium}}{2} \]
  \[L_{trapesium}=\frac{10 + 15 \times 12}{2} \]
  \[L_{trapesium}=150 \;cm^{2} \]
Sehingga, luas permukaan prisma adalah
  \[L_{prisma} = \left( 2 \times L_{alas} \right)+ \left( K_{alas} \times t_{prisma} \right)\]
  \[L_{prisma} = \left( 2 \times L_{trapesium}\right) + \left( K_{trapesium} \times t_{prisma} \right)\]
  \[L_{prisma} = \left( 2 \times 150 \right) + \left( 50 \times 9 \right)\]
  \[L_{prisma} = 300 + 450 = 750 \; cm^{2}\]
Jawaban: D

Contoh 2 – Soal Bangun Ruang Sisi Datar
Seorang pedagang ikan hias ingin membuat sebuah kerangka akuarium dengan menggunakan aluminium. Kerangka tersebut berbentuk balok dengan ukuran 2 m × 1 m × 50 cm. Jika harga aluminium Rp30.000,00 per meter, maka biaya yang diperlukan untuk membuat kerangka akuarium tersebut adalah …. (SOAL UN Matematika SMP 2016)
A.       Rp600.000,00
B.       Rp450.000,00
C.       Rp420.000,00
D.       Rp105.000,00
Pembahasan:
Berdasarkan soal cerita di atas, kita dapat mengetahui bahwa akuarium tersebut berbentuk balok dengan ukuran berikut.
Panjang = 2 m
Lebar = 1 m
Tinggi = 50 cm = 0,5 m

Panjang total kerangka balok adalah
= 4 x 2 + 4 x 1 + 4 x 0,5
= 8 + 4 + 2 = 14 m
 Biaya yang diperlukan untuk membuat kerangka akuarium
= 14 m × Rp30.000,00 = Rp420.000,00
Jawaban: C
Demikianlah ulasan materi terkait bangun ruang sisi datar yang meliputi kubus, balok, prisma, dan limas. Bahasan utama dalam materi adalah meliputi rumus volume bangun ruang datar dan luas permukaan bangun ruang datar. Terimakasih sudah mengunjungi atikroest, semoga bermanfaat.

Komentar

Posting Komentar

Postingan populer dari blog ini

MATRIKS

Gambar
Pengertian Matriks Matriks adalah susunan simbol, ekspresi, bilangan real, bilangan kompleks atau elemen-elemen yang tersusun dalam kolom dan baris sehingga membentuk suatu bangun persegi atau bisa juga berbentuk persegi panjang.  Sebuah matriks diberi nama dengan huruf kapital, contohnya seperti matriks A, matriks B, matriks C, dan seterusnya. Sedangkan isi di dalam matriks atau anggotanya dinyatakan dengan huruf kecil seperti a, b, c, d, dan seterusnya. Nah, dalam matriks ini juga dikenal istilah ordo, yaitu banyaknya jumlah baris dan kolom dalam matriks.  Anggota atau isi di dalam matriks juga bisa dinyatakan dengan huruf kecil yang memiliki indeks ganda seperti aif. Indeks pertama mengindikasikan baris horizontal tempat anggota tersebut berada, sedangkan indeks kedua mengindikasikan kolom vertikal tempat anggota matriks tersebut berada.   Contohnya seperti a12 berarti anggota a berada di baris pertama dan di kolom kedua. Contoh lainnya b36 yang artinya anggota b berada di baris ket
Baca selengkapnya

Peluang

Gambar
Peluang Peluang dapat diartikan sebagai kesempatan. Materi peluang suatu kejadian artinya kemungkinan yang dapat terjadi dari sebuah kejadian. Peluang suatu kejadian dapat berupa menang atau gagal. Peluang untuk menang artinya kesempatan untuk menang. Peluang gagal artinya kemungkian tidak terjadi suatu kejadian yang diharapkan. Jumlah peluang terjadi dan tidak terjadi adalah 1 (satu). Misallkan peluang kejadian akan turun hujan adalah   maka peluang kejadian tidak akan turun hujan adalah  . Nilai peluang bergantung dari jumlah ruang sampel dan banyaknya kemungkinan yang dapat terjadi. Peluang juga bergantung pada banyaknya percobaan. Percobaan adalah kejadian yang memungkinkan terjadi kemungkinan-kemungkinan tertentu. Penerapan peluang dalam kehidupan sehari-hari dapat dilihat di bidang asuransi. Titik Sampel dan Ruang Sampel Ruang sampel adalah himpunan semua hasil yang mungkin terjadi dari suatu percobaan. Titik sampel adalah semua anggota yang berada pada ruang sampel. Untu
Baca selengkapnya

Permutasi dan Kombinasi

Gambar
Permutasi dan kombinasi adalah dua cara berbeda untuk menyusun suatu himpunan. Tidak jarang siswa bingung dalam membedakan keduanya. Ketika urutan diperhatikan, itulah permutasi. Ketika urutan tidak diperhatikan, itulah kombinasi. Mari kita pahami bersama apa perbedaan permutasi dan kombinasi dengan contoh berikut: Terdapat suatu lomba dengan dua babak yaitu babak penyisihan dan babak final. Pada babak penyisihan dipilih 5 peserta terbaik yang akan melanjutkan ke babak final, pemilihan ini dapat disebut sebagai kombinasi, karena posisi ke-1, ke-2, ke-3, ke-4, dan ke-5 dari 5 peserta yang dipilih tidak diperhatikan. Selanjutnya pada babak final akan dipilih juara 1, juara 2, dan juara 3, pemilihan ini disebut sebagai permutasi, karena dari 3 peserta yang dipilih sebagai juara, posisi ke-1, ke-2, dan ke-3 dari 3 peserta yang dipilih diperhatikan. Lalu bagaimana cara menghitung banyaknya susunan yang mungkin dari permutasi dan kombinasi pada contoh di atas? Yuk simak penjelasannya di baw
Baca selengkapnya