Pola bilangan
Pola baris bilangan
Suku ke-n menunjuk pada suku pada urutan ke-n, lebih jelasnya dapat dilihat pada gambar berikut.

Rumus suku ke-n pada Barisan Aritmetika
Jumlah n suku pertama pada barisan aritmetika
Penjumlahan suku-suku pada barisan geometri membentuk sebuah deret yang disebut dengan deret geometri.

Rumus di bawah dapat digunakan untuk mencari jumlah n suku pertama.
Jumlah n suku pertama pada Barisan Geometri
untuk r > 1
Contoh Soal dan Pembahasan
Seutas tali dipotong menjadi 5 bagian yang ukurannya membentuk deret geometri. Jika panjang potongan tali terpendek 4 cm dan panjang potongan tali terpanjang 324 cm, maka panjang tali semula adalah …. (SOAL UN MATEMATIKA SMP 2016)
A. 328 cm
B. 484 cm
C. 648 cm
D. 820 cm
Pembahasan:
Tali membuat Barisan geometri seperti terlihat pada gambar di bawah.

dengan
 adalah tali terpendek = 4 cm
adalah tali terpendek = 4 cm
 adalah sampai terpanjang = 324 cm
adalah sampai terpanjang = 324 cm
Sehingga,
- Pola bilangan asli: 1, 2, 3, 4, 5, …
Pola bilangan: n, n bilangan asli - Pola bilangan ganjil: 1, 3, 5, 7, …
Pola bilangan:, n bilangan asli
- Pola bilangan genap: 2, 4, 6, 8, …
Pola bilangan: 2n, n bilangan asli - Pola bilangan persegi: 1, 4, 9, 16, …
Pola bilangan:, n bilangan asli

- Pola bilangan segitiga: 1, 3, 6, 10, …
Pola bilangan: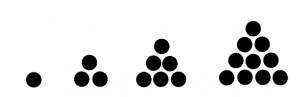
Baris dan deret dalam pembelajaran Matematika SMP dibedakan menjadi dua yaitu aritmetika dan geometri. Materi baris dan deret aritmetika dan geometri berguna untuk memudahkan dalam menghitung sejumlah tertentu. Pastinya secara lebih cepat. Contohnya adalah menjumlahkan bilangan 1 sampai dengan 100. Coba hitung! Apakah jawaban yang kalian peroleh adalah 5050? Berapa waktu yang sobat butuhkan untuk menghitungnya? Jika menghitung secara manual, pasti akan memakan waktu yang lama. Sekarang coba perhatikan TRIK berikut.
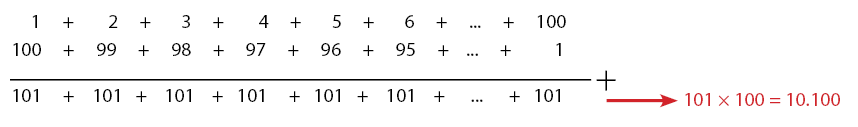
Perhatikan keunikan pada penjumlahan tiap kolom di atas. Seluruh kolom pada baris di atas, jumlah masing-masingnya adalah 101. Hasil di atas membentuk bilangan 101 sejumlah 100 kali. Dengan mudah, kita bisa mendapatkan hasilnya yaitu . Bilangan 101 sejumlah 100 kali terbentuk dari dua buah deret. Untuk mengetahui jumlah satu deretnya, hasil akhirnya perlu dibagi dua.
. Bilangan 101 sejumlah 100 kali terbentuk dari dua buah deret. Untuk mengetahui jumlah satu deretnya, hasil akhirnya perlu dibagi dua.
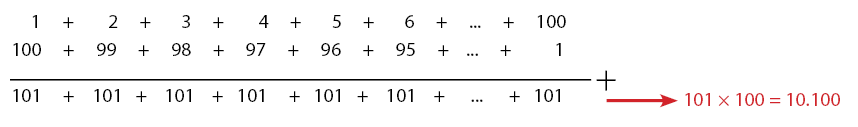
Perhatikan keunikan pada penjumlahan tiap kolom di atas. Seluruh kolom pada baris di atas, jumlah masing-masingnya adalah 101. Hasil di atas membentuk bilangan 101 sejumlah 100 kali. Dengan mudah, kita bisa mendapatkan hasilnya yaitu
Begitulah cara cepat untuk mengetahui jumlah bilangan 1 sampai dengan 100. Selanjutnya, ilmu ini berkembang menjadi baris dan deret. Pembahasan mengenai masing-masing jenis baris dan deret dapat disimak pada pembahasan di bawah.
Aritmetika
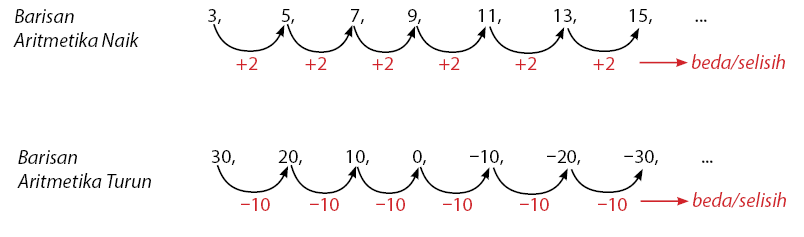
Barisan Aritmetika mempunyai ciri-ciri yaitu selisih/beda antara dua suku yang berurutan selalu sama atau tetap. Perhatikan dua contoh barisan Aritmetika di bawah yang meliputi barisan aritmerika naik dan barisan aritmetika turun.

Suku ke-n menunjuk pada suku pada urutan ke-n, lebih jelasnya dapat dilihat pada gambar berikut.

Berdasarkan pola barisan aritmetika, terdapat rumus yang dapat digunakan untuk mempermudah mencari suku ke-n.
Rumus suku ke-n pada Barisan Aritmetika
Keterangan:
 = suku ke-n
= suku ke-n
a = suku pertama
b = beda/selisih
a = suku pertama
b = beda/selisih
Penjumlahan suku-suku pada barisan aritmetika membentuk sebuah deret yang disebut dengan deret aritmetika.

Rumus di bawah dapat digunakan untuk mencari jumlah n suku pertama.

Rumus di bawah dapat digunakan untuk mencari jumlah n suku pertama.
Jumlah n suku pertama pada barisan aritmetika
atau
Keterangan:
 = jumlah n suku pertama
= jumlah n suku pertama
 = suku ke-n
= suku ke-n
a = suku pertama
b = beda/selisih
a = suku pertama
b = beda/selisih
Geometri
Barisan Geometri mempunyai ciri-ciri memiliki perbandingan/rasio antara dua suku yang berurutan selalu sama atau tetap. Perhatikan dua contoh barisan Geometri di bawah yang meliputi barisan geometri naik dan barisan geometri turun.
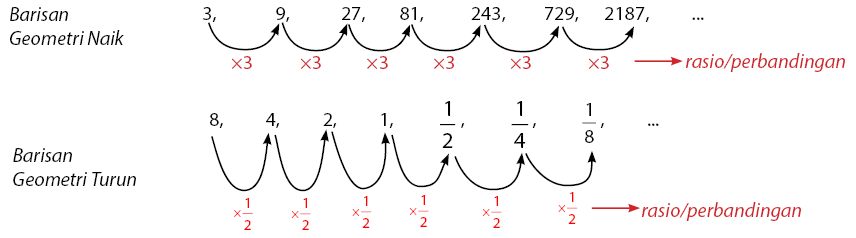
Suku ke-n menunjuk pada suku pada urutan ke-n, lebih jelasnya dapat dilihat pada gambar berikut.


Suku ke-n menunjuk pada suku pada urutan ke-n, lebih jelasnya dapat dilihat pada gambar berikut.

Berdasarkan pola barisan aritmetika, terdapat rumus yang dapat digunakan untuk mempermudah mencari suku-n.
Rumus suku ke-n pada Barisan Geometri
Rumus suku ke-n pada Barisan Geometri
Keterangan:
 = suku ke-n
= suku ke-n
a = suku pertama
r = rasio
a = suku pertama
r = rasio
Penjumlahan suku-suku pada barisan geometri membentuk sebuah deret yang disebut dengan deret geometri.

Rumus di bawah dapat digunakan untuk mencari jumlah n suku pertama.
Jumlah n suku pertama pada Barisan Geometri
untuk r > 1
untuk r < 1
Keterangan:
 = jumlah n suku pertama
= jumlah n suku pertama
 = suku ke-n
= suku ke-n
a = suku pertama
r = rasio =
a = suku pertama
r = rasio =
Contoh Soal dan Pembahasan
Seutas tali dipotong menjadi 5 bagian yang ukurannya membentuk deret geometri. Jika panjang potongan tali terpendek 4 cm dan panjang potongan tali terpanjang 324 cm, maka panjang tali semula adalah …. (SOAL UN MATEMATIKA SMP 2016)
A. 328 cm
B. 484 cm
C. 648 cm
D. 820 cm
Pembahasan:
Tali membuat Barisan geometri seperti terlihat pada gambar di bawah.
dengan
Sehingga,
Sehingga barisan geometrinya menjadi 4, 12, 36, 108, dan 324.
Panjang tali semula adalah 4 + 12 + 36 + 108 + 324 = 484 cm.
Jawaban: B

Panjang tali semula adalah 4 + 12 + 36 + 108 + 324 = 484 cm.
Jawaban: B
Simak kumpulan soal UN dengan materi pola barisan dan bilangan pada pembahasan di bawah.
BAGIAN I
Contoh 1: Soal UN Matematika Tahun 2015
Diketahui barisan bilangan:
Diketahui barisan bilangan:
Suku ke-32 adalah ….
A. 465
B. 168
C. 158
D. 153
A. 465
B. 168
C. 158
D. 153
Pembahasan:
Berdasarkan pola bilangan pada soal, dapat diperoleh bawah suku pertamanya adalah 3 (a = 3) dan beda setiap sukunya adalah 5 (b = 5).
Berdasarkan pola bilangan pada soal, dapat diperoleh bawah suku pertamanya adalah 3 (a = 3) dan beda setiap sukunya adalah 5 (b = 5).
Jawaban: C
Contoh 2: Soal UN Matematika Tahun 2013
Diketahui barisan bilangan
Diketahui barisan bilangan
Suku ke-52 adalah …
A. 201
B. 207
C. 208
D. 215
A. 201
B. 207
C. 208
D. 215
Pembahasan:
Berdasarkan pola bilangan pada soal, dapat diperoleh bawah suku pertamanya adalah -3 (a = -3) dan beda setiap sukunya adalah 4 (b = 4).
Berdasarkan pola bilangan pada soal, dapat diperoleh bawah suku pertamanya adalah -3 (a = -3) dan beda setiap sukunya adalah 4 (b = 4).
Jawaban: A
Contoh 3: Soal UN Matematika Tahun 2012
Dua suku berikutnya dari barisan di bawah
Dua suku berikutnya dari barisan di bawah
Adalah ….
A. 13, 18
B. 13, 17
C. 12, 26
D. 12, 15
A. 13, 18
B. 13, 17
C. 12, 26
D. 12, 15
Pembahasan:
Perhatikan pola barisan berikut.

Jawaban: A
Perhatikan pola barisan berikut.

Jawaban: A
Contoh 4: Soal UN Matematika Tahun 2010
Dua suku berikutnya dari barisan bilangan
Dua suku berikutnya dari barisan bilangan
adalah ….
A. 24, 15
B. 24, 16
C. 25, 17
D. 25, 18
A. 24, 15
B. 24, 16
C. 25, 17
D. 25, 18
Pembahasan:

Jawaban: A

Jawaban: A
Contoh 5: Soal UN Matematika Tahun 2008
Suku ke-22 dari barisan di bawah
Suku ke-22 dari barisan di bawah
adalah ….
A. –27
B. –21
C. –15
D. –9
A. –27
B. –21
C. –15
D. –9
Pembahasan:
Berdasarkan pola bilangan pada soal, dapat diperoleh bawah suku pertamanya adalah 99 (a = 99) dan beda setiap sukunya adalah -6 (b = -6).
Berdasarkan pola bilangan pada soal, dapat diperoleh bawah suku pertamanya adalah 99 (a = 99) dan beda setiap sukunya adalah -6 (b = -6).
Jawaban: A
BAGIAN II
Contoh 1: Soal UN Matematika Tahun 2009
Budi sedang menumpuk kursi yang tingginya masing-masing 90 cm. Tinggi tumpukan 2 kursi 96 cm, dan tinggi tumpukan 3 kursi 102 cm. Tinggi tumpukan 10 kursi adalah ….
A. 117 cm
B. 120 cm
C. 144 cm
D. 150 cm
Budi sedang menumpuk kursi yang tingginya masing-masing 90 cm. Tinggi tumpukan 2 kursi 96 cm, dan tinggi tumpukan 3 kursi 102 cm. Tinggi tumpukan 10 kursi adalah ….
A. 117 cm
B. 120 cm
C. 144 cm
D. 150 cm
Pembahasan:
Pola tumpukan
2 kursi tinggi 96 cm
tinggi 96 cm
3 kursi tinggi 102 cm
tinggi 102 cm
Perhatikan bahwa setiap penambahan 1 kursi, tingginya bertambah 6 cm.
Sehingga,
4 kursi tinggi 108 cm
tinggi 108 cm
5 kursi tinggi 114 cm
tinggi 114 cm
6 kursi tinggi 120 cm
tinggi 120 cm
7 kursi tinggi 126 cm
tinggi 126 cm
8 kursi tinggi 132 cm
tinggi 132 cm
9 kursi tinggi 138 cm
tinggi 138 cm
10 kursi tinggi 144 cm
tinggi 144 cm
Pola tumpukan
2 kursi
3 kursi
Perhatikan bahwa setiap penambahan 1 kursi, tingginya bertambah 6 cm.
Sehingga,
4 kursi
5 kursi
6 kursi
7 kursi
8 kursi
9 kursi
10 kursi
Jadi, tinggi tumpukan 10 kursi adalah 144 cm.
Jawaban: C
Jawaban: C
Contoh 2: Soal UN Matematika Tahun 2007
Pada tumpukan batu bata, banyak batu bata paling atas ada 8 buah, tepat di bawahnya ada 10 buah, dan seterusnya setiap tumpukan di bawahnya selalu lebih banyak 2 buah dari tumpukan di atasnya. Jika ada 15 tumpukan batu bata (dari atas sampai bawah), berapa banyak batu bata pada tumpukan paling bawah?
A. 35 buah
B. 36 buah
C. 38 buah
D. 40 buah
Pada tumpukan batu bata, banyak batu bata paling atas ada 8 buah, tepat di bawahnya ada 10 buah, dan seterusnya setiap tumpukan di bawahnya selalu lebih banyak 2 buah dari tumpukan di atasnya. Jika ada 15 tumpukan batu bata (dari atas sampai bawah), berapa banyak batu bata pada tumpukan paling bawah?
A. 35 buah
B. 36 buah
C. 38 buah
D. 40 buah
Pembahasan:
Perhatikan pola tumpukan batu bata pada tabel di bawah.
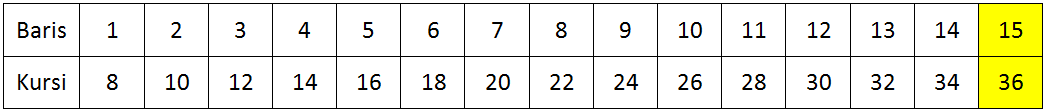
Perhatikan pola tumpukan batu bata pada tabel di bawah.
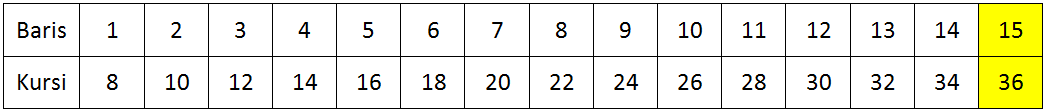
Jadi, banyak batu bata pada tumpukan paling bawah adalah 36 buah.
Jawaban: B
Jawaban: B
Contoh 3: Soal UN Matematika Tahun 2006
Dalam gedung pertunjukkan disusun kursi dengan baris paling depan terdiri dari 12 buah, baris kedua berisi 14 buah, baris ketiga 16 buah dan seterusnya selalu bertambah 2. Banyaknya kursi pada baris ke-20 adalah ….
A. 28 buah
B. 50 buah
C. 58 buah
D. 60 buah
Dalam gedung pertunjukkan disusun kursi dengan baris paling depan terdiri dari 12 buah, baris kedua berisi 14 buah, baris ketiga 16 buah dan seterusnya selalu bertambah 2. Banyaknya kursi pada baris ke-20 adalah ….
A. 28 buah
B. 50 buah
C. 58 buah
D. 60 buah
Pembahasan:
Pola barisan kursi adalah sebagai berikut.
Baris 1 12 buah
12 buah
Baris 2 14 buah
14 buah
Baris 3 16 buah
16 buah
Setiap baris akan bertambah 2 buah kursi, sehingga pola berikutnya adalah
Baris 4 18 buah
18 buah
Baris 5 20 buah
20 buah
Baris 6 22 buah
22 buah
Baris 7 24 buah
24 buah
Baris 8 26 buah
26 buah
Baris 9 28 buah
28 buah
Baris 10 30 buah
30 buah
Baris 11 32 buah
32 buah
Baris 12 34 buah
34 buah
Baris 13 36 buah
36 buah
Baris 14 38 buah
38 buah
Baris 15 40 buah
40 buah
Baris 16 42 buah
42 buah
Baris 17 44 buah
44 buah
Baris 18 46 buah
46 buah
Baris 19 48 buah
48 buah
Baris 20 50 buah
50 buah
Pola barisan kursi adalah sebagai berikut.
Baris 1
Baris 2
Baris 3
Setiap baris akan bertambah 2 buah kursi, sehingga pola berikutnya adalah
Baris 4
Baris 5
Baris 6
Baris 7
Baris 8
Baris 9
Baris 10
Baris 11
Baris 12
Baris 13
Baris 14
Baris 15
Baris 16
Baris 17
Baris 18
Baris 19
Baris 20
Cara yang dilakukan di atas tidak efektif. Ada cara lain yang dapat digunakan untuk menentukan banyak kursi pada baris ke-20 yaitu dengan rumus suku ke-n pada barisan aritmetika.
Diketahui: a = 12 dan b = 2, maka
Diketahui: a = 12 dan b = 2, maka
Jadi, banyaknya kursi pada baris ke-20 adalah 50 buah.
Jawaban: B
Jawaban: B
BAGIAN III
Contoh 1: Soal UN Matematika Tahun 2013
Diketahui barisan bilangan 8, 4, 2, 1, …
Rumus suku ke-n barisan tersebut adalah ….
Diketahui barisan bilangan 8, 4, 2, 1, …
Rumus suku ke-n barisan tersebut adalah ….
Pembahasan:
Untuk mendapatkan jawaban yang sesuai, kita akan selidiki rumus suku ke-n yang diberikan pada pilihan ganda.
Pilihan A:
Untuk mendapatkan jawaban yang sesuai, kita akan selidiki rumus suku ke-n yang diberikan pada pilihan ganda.
Pilihan A:
Pilihan B: 
Pilihan C: 
Pilihan C sesuai untuk pola yang diberikan.
Jawaban: C
Jawaban: C
Contoh 2: Soal UN Matematika Tahun 2012
Amoeba membelah diri menjadi dua setiap 20 menit. Jika mula-mula terdapat 15 amoeba, maka setelah 2 jam banyak amoeba menjadi ….
A. 2.120
B. 1.920
C. 960
D. 480
Amoeba membelah diri menjadi dua setiap 20 menit. Jika mula-mula terdapat 15 amoeba, maka setelah 2 jam banyak amoeba menjadi ….
A. 2.120
B. 1.920
C. 960
D. 480
Pembahasan:
Periode pembelahan amoeba adalah
Periode pembelahan amoeba adalah
Proses pembelahan:
Periode 0 15 amoeba
15 amoeba
Periode 1 30 amoeba
30 amoeba
Periode 2 60 amoeba
60 amoeba
Periode 3 120 amoeba
120 amoeba
Periode 4 240 amoeba
240 amoeba
Periode 5 480 amoeba
480 amoeba
Periode 6 960 amoeba
960 amoeba
Jadi, banyaknya amoeba setelah 2 jam adalah 960
Jawaban: C
Periode 0
Periode 1
Periode 2
Periode 3
Periode 4
Periode 5
Periode 6
Jadi, banyaknya amoeba setelah 2 jam adalah 960
Jawaban: C
Contoh 3: Soal UN Matematika Tahun 2010
Perhatikan gambar pola di bawah.

Banyak lingkaran pada pola ke–20 adalah….
A. 380
B. 420
C. 462
D. 506
Perhatikan gambar pola di bawah.

Banyak lingkaran pada pola ke–20 adalah….
A. 380
B. 420
C. 462
D. 506
Pembahasan:
Banyaknya lingkaran yang menyusun persegi panjang mengikuti pola di bawah.
Pola ke-1 2 lingkaran
2 lingkaran
Pola ke-2 6 lingkaran
6 lingkaran
Pola ke-3 12 lingkaran
12 lingkaran
Pola ke-4 20 lingkaran
20 lingkaran
Perhatikan pola yang dibentuk seperti gambar di bawah.

Pola barisan tersebut membentuk rumus suku ke-n seperti di bawah.
Banyaknya lingkaran yang menyusun persegi panjang mengikuti pola di bawah.
Pola ke-1
Pola ke-2
Pola ke-3
Pola ke-4
Perhatikan pola yang dibentuk seperti gambar di bawah.

Pola barisan tersebut membentuk rumus suku ke-n seperti di bawah.
Sehingga, suku ke-20 nya adalah
Jawaban: B
Contoh 4: Soal UN Matematika Tahun 2008
Perhatikan gambar di bawah!
Perhatikan gambar di bawah!

Banyak lingkaran pada pola ke-10 adalah….
A. 99 buah
B. 104 buah
C. 115 buah
D. 120 buah
A. 99 buah
B. 104 buah
C. 115 buah
D. 120 buah
Pembahasan:
Banyaknya lingkaran yang menyusun persegi panjang mengikuti pola di bawah.
Pola ke-1 3 lingkaran
3 lingkaran
Pola ke-2 8 lingkaran
8 lingkaran
Pola ke-3 15 lingkaran
15 lingkaran
Pola ke-4 24 lingkaran
24 lingkaran
Perhatikan pola yang dibentuk mengikuti pola rumus suku ke-n .
.
Jadi, banyaknya lingkaran pada pola ke-10 adalah
Banyaknya lingkaran yang menyusun persegi panjang mengikuti pola di bawah.
Pola ke-1
Pola ke-2
Pola ke-3
Pola ke-4
Perhatikan pola yang dibentuk mengikuti pola rumus suku ke-n
Jadi, banyaknya lingkaran pada pola ke-10 adalah
Jawaban: D
Contoh 5: Soal UN Matematika Tahun 2005
Rumus suku ke-n dari barisan bilangan
Rumus suku ke-n dari barisan bilangan
adalah ….
Pembahasan:
Berdasarkan pilihan ganda yang diberikan hanya satu kemungkinan rumus suku ke-n yang dapat menghasilkan nilai 0 (nol) pada pola pertamanya, yaitu (n – 1)(n + 2). Jadi, rumus suku ke-n dari barisan bilangan
Berdasarkan pilihan ganda yang diberikan hanya satu kemungkinan rumus suku ke-n yang dapat menghasilkan nilai 0 (nol) pada pola pertamanya, yaitu (n – 1)(n + 2). Jadi, rumus suku ke-n dari barisan bilangan
adalah (n – 1)(n + 2)
Jawaban: C
Sekian materi pola bilangan, baris dan deret untuk tingkat smp. Terimakasih sudah mengunjungi atikroest.blogspot.com semoga bermanfaat!Jawaban: C
Komentar
Posting Komentar