Kesebangunan dan Kekongruenan (soal dan pembahasan)

Kesebangunan dan Kekongruenan

Hallo sobat atikroest, pada halaman ini akan mengupas tentang contoh soal kesebangunan dan kekongruenan. Seperti kisi-kisi yang telah dikeluarkan BSNP, materi kesebangunan dan kekongruenan akan kembali muncul di ujian nasional. Kisi-kisi untuk kesebangunan dan kekongruenan diberikan dalam 3 (tiga) level kognitif, yaitu pengetahuan dan pemahaman, aplikasi, dan penalaran. Halaman ini akan membahas kisi-kisi UN 2019 dengan materi kesebangunan dan kekongruenan untuk level pengetahuan dan pemahaman.
Simak kumpulan soal UN dengan materi kesebangunan dan kekongruenan pada pembahasan di bawah.

BAGIAN I
Contoh 1: Soal UN Matematika SMP/MTS Tahun 2014
Perhatikan gambar!
pasangan segitiga yang sebagun
Banyak pasangan segitiga yang kongruen adalah ….
A.     1
B.     2
C.     3
D.     4

Pembahasan:
Banyak pasangan segitiga yang kongruen ada 2 pasang, yaitu
  \[ ABC \; \textrm{dan} \; ABD \]
  \[ BCE \; \textrm{dan} \; ADE \]
Jawaban: B


Contoh 2: Soal UN Matematika SMP/MTS Tahun 2013

Diketahui \Delta ABC dan \Delta DEF kongruen, besar \angle A = 37^{o}, \angle B = \angle E, dan \angle F = 92^{o}. Persamaan sisi yang sama panjang adalah ….
A.     AB = DF
B.     AB = DE
C.     BC = DF
D.     AC = EF

Pembahasan:
Perhatikan gambar di bawah!
dua segitiga yang kongruen
Pada dua segitiga yang kongruen, panjang sisi suatu segitiga berhubungan dengan sudut yang menghadap sisi tersebut. Misalnya, panjang sisi dengan sudut 37^{o} di segitiga pertama akan memiliki panjang sisi yang sama dengan sudut 37^{o} pada segitiga ke dua.
Jadi, persamaan sisi yang sama panjang adalah AB = DE, CB = EF, dan AC = DF.
Jawaban: B

Contoh 3: Soal UN Matematika SMP/MTS Tahun 2013


Segitiga ABC dengan panjang sisi 6 cm, 8 cm dan 12 cm sebangun dengan segitiga DEF yang panjang sisinya 12 cm, 9 cm dan 18 cm. Perbandingan sisi-sisi segitiga ABC dan segitiga DEF adalah ….
A.     3 : 4
B.     2 : 3
C.     1 : 2
D.     1 : 3

Pembahasan:
Urutan sisi-sisi segitiga ABC dari yang terpendek adalah 6 cm, 8 cm, dan 12 cm.
Urutan sisi-sisi segitiga DEF dari yang terpendek adalah 9 cm, 12 cm, dan 18 cm.
Pada segitiga yang sebangun, sisi-sisi yang bersesuaian akan sebanding.
Perbandingan sisi tersebut dinyatakan dalam persamaan di bawah.
  \[ \frac{6}{9} = \frac{8}{12} = \frac{12}{18} = \frac{2}{3} \]
Jawaban: B


Contoh 4: Soal UN Matematika SMP/MTS Tahun 2009

Pada gambar di samping, segitiga ABC kongruen dengan segitiga DEF.
contoh matematika kesebangunan dan kekongruenan
Panjang EF adalah ….
A.     5 cm
B.     6 cm
C.     6,5 cm
D.     7 cm

Pembahasan:
Segitiga pada soal merupakan dua segitiga yang kongruen. Sisi EF bersesuaian dengan sudut dengan tanda \circ. Jadi, panjang sudut EF adalah 7 cm.
Jawaban: D

Contoh 5: Soal UN Matematika SMP/MTS Tahun 2008

Perhatikan gambar di samping!
soal un kesebangunan
Panjang BC adalah ….
A.     24 cm
B.     18 cm
C.     12 cm
D.     9 cm

Pembahasan:
Perhatikan kembali gambar di bawah!
Contoh Soal UN Matematika SMP Kesebangunan dan Kekongruenan
Dua perbandingan antara segitiga APQ dan ABC akan menghasilkan persamaan di bawah.
  \[ \frac{AP}{PQ} = \frac{AB}{BC} \]
  \[ \frac{4}{6} = \frac{12}{BC} \]
  \[ 4BC = 72 \]
  \[ BC = \frac{60}{4} = 18 \; cm \]
Jadi, panjang BC adalah 18 cm.
Jawaban: B


Contoh 6: Soal UN Matematika SMP/MTS Tahun 2008

Perhatikan gambar!
Contoh Soal UN Matematika SMP Kesebangunan dan Kekongruenan
Segitiga ABC dan DEF kongruen. Di antara pernyataan berikut, yang benar adalah ….
  \[ \textrm{A.} \; \; \; \angle B = \angle E \; \textrm{dan} \; AB = DE \]
  \[ \textrm{B.} \; \; \; \angle C = \angle D \; \textrm{dan} \; AB = DE \]
  \[ \textrm{C.} \; \; \; \angle B = \angle E \; \textrm{dan} \; CB = DF \]
  \[ \textrm{D.} \; \; \; \angle C = \angle D \; \textrm{dan} \; CB = DF \]

Pembahasan:
Dua segitiga dikatakan kongruen jika kedua segitiga tersebut sama dan sebangun. Pernyataan yang benar dari segitiga ABC dan DEF adalah
  \[ \angle C = \angle D \]
  \[ CB = DF \]
Jawaban: D


Contoh 7: Soal UN Matematika SMP/MTS Tahun 2007

Perhatikan gambar berikut!
Soal un kesebangunan dan kekongruenan
Panjang TQ adalah ….
A.     4 cm
B.     5 cm
C.     6 cm
D.     7 cm

Pembahasan:
  \[ \frac{TQ}{ST} = \frac{QP}{PR} \]
  \[ \frac{TQ}{8} = \frac{3 + TQ}{12} \]
  \[ 12TQ = 8 \left( 3 + TQ \right) \]
  \[ 12TQ = 24 + 8TQ \]
  \[ 12TQ - 8TQ = 24 \]
  \[ 4TQ = 24 \]
  \[ TQ = \frac{24}{4} = 6 \; cm \]
Jawaban: C


Contoh 8: Soal UN Matematika SMP/MTS Tahun 2006


Perhatikan gambar berikut ini!
Segitiga sebangun
Pada segitiga PQR, QT adalah garis bagi sudut Q, ST \perp QR. Segitiga yang kongruen adalah ….
  \[ \textrm{A.} \; \; \; \Delta PTU \; \textrm{dan} \; \Delta RTS \]
  \[ \textrm{B.} \; \; \; \Delta QUT \; \textrm{dan} \; \Delta PTU \]
  \[ \textrm{C.} \; \; \; \Delta QTS \; \textrm{dan} \; \Delta RTS \]
  \[ \textrm{D.} \; \; \; \Delta TUQ \; \textrm{dan} \; \Delta TQR \]
Pembahasan:
Dua segitiga dikatakan kongruen jika kedua segitiga tersebut sama dan sebangun.
Segitiga yang kongruen adalah $
  \[ \Delta PTU \; \textrm{dan} \; \Delta RTS \]
Jawaban: A

Contoh 9: Soal UN Matematika SMP/MTS Tahun 2006

Perhatikan gambar berikut ini!
Soal UN Matematika SMP Kesebangunan dan Kekongruenan
Nilai x adalah ….
A.     1,5
B.     6
C.     8
D.     10

Pembahasan:
  \[ \frac{BE}{EF} = \frac{BA}{AC} \]
  \[ \frac{x}{6} = \frac{2 + x}{8} \]
  \[ 8x = 6 \left( 2 + x \right) \]
  \[ 8x = 12 + 6x \]
  \[ 8x - 6x = 12 \]
  \[ 2x = 12 \]
  \[ x = \frac{12}{2} = 6 \; cm \]
Jawaban: B

BAGIAN II

Contoh 1: Soal UN MATEMATIKA SMP 2016

Febri mempunyai tinggi badan 150 cm. Ia berdiri pada titik yang berjarak 10 m dari sebuah gedung. Ujung bayangan Febri berimpit dengan ujung bayangan gedung. Jika panjang bayangan Febri adalah 4 m, maka tinggi gedung adalah ….
A.     5,25 m
B.     5,50 m
C.     6,25 m
D.     6,75 m
Pembahasan:
Perhatikan gambar berikut!
kesebangunan dan kekongruenan
Perhatikan segitiga ABE dan segitiga ACD!
Berdasarkan prinsip kesebangunan dapat diperoleh 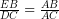\frac{EB}{DC} = \frac{AB}{AC}
Sehingga,
  \[\frac{1,5}{DC} = \frac{4}{14} \]
  \[DC = \frac{1,5 \times 14}{4} \]
  \[DC = 5,25 \; m \]
Jawaban: A

Contoh 2: Soal UN Matematika SMP/MTS Tahun 2014

Perhatikan gambar di samping!
Contoh soal UN Matematika SMP/MTs
Panjang TR adalah ….
A.     2 cm
B.     3 cm
C.     4 cm
D.     5 cm
Pembahasan:
  \[ \frac{PS}{TP} = \frac{PR}{PQ} \]
  \[ \frac{9}{12} = \frac{12 + TR}{20} \]
  \[ 12 \left( 12 + TR \right) = 9 \times 20 \]
  \[ 144 + 12TR = 180 \]
  \[ 12 TR = 180 - 144 \]
  \[ 12 TR = 36 \]
  \[ TR = \frac{36}{12} = 3 \; cm \]
Jawaban: B

Contoh 3: Soal UN Matematika SMP/MTS Tahun 2010

Sebuah foto berukuran tinggi 30 cm dan lebar 20 cm ditempel pada sebuah karton. Sisa karton di sebelah kiri, kanan, atas foto 2 cm. jika foto dan karton sebangun, sisa karton di bawah foto adalah …
A.     5 cm
B.     4 cm
C.     3 cm
D.     2 cm
Pembahasan:
Perhatikan gambar di bawah!
Soal kesebangunan dan kekongruenan
Menccari sisa karton di bawah foto:
  \[ \frac{20}{24} = \frac{30}{32 + x} \]
  \[ 20 \left( 32 + x \right) = 30 \times 24 \]
  \[ 640 + 20x = 720 \]
  \[ 20x = 720 - 640 \]
  \[ 20x = 80 \]
  \[ x = \frac{80}{20} = 4 \; cm \]
Jawaban: B

Contoh 4: Soal UN Matematika SMP/MTS Tahun 2009

Sebuah gedung mempunyai panjang bayangan 56 m di atas tanah mendatar. Pada saat yang sama seorang siswa dengan tinggi 1,5 m mempunyai bayangan 3,5 m. Tinggi gedung sebenarnya adalah …
A.     18 m
B.     21 m
C.     22 m
D.     24 m
Pembahasan:
Perhatikan gambar di bawah!
soal un kesebangunan
Mencari tinggi gedung:
  \[ \frac{x}{1,5} = \frac{56}{3,5} \]
  \[ 3,5x = 56 \times 1,5 \]
  \[ 3,5x = 84 \]
  \[ x = \frac{84}{3,5} \]
  \[ x = 24 \; m \]
Jadi, tinggi gedung tersebut adalah 24 meter.
Jawaban: D

BAGIAN III

Contoh 1: Soal UN MATEMATIKA SMP 2016

Perhatikan gambar berikut!
kesebangunan dan kekongruenan
Jika CF : FB = 2 : 3 dan CD = 12 cm, maka panjang EF adalah ….
A.     6 cm
B.     9 cm
C.     12 cm
D.     18 cm
Pembahasan:
Berdasarkan keterangan pada soal, kita dapat mengetahui ukuran masing-masing sisi, seperti terlihat pada gambar berikut.
kesebangunan dan kekongruenan
Untuk menghitung EF, gunakan rumus di bawah.
  \[EF =\frac{CD \times FB + AB \times CF}{FB + CF} \]
Sehingga,
  \[EF =\frac{12 \times 3x + 27 \times 2x}{3x + 2x} \]
  \[EF =\frac{36x + 54x}{5x} \]
  \[EF =\frac{90x}{5x}\;=\;18\;cm \]
Jawaban: D

Contoh 2: SOAL UN MATEMATIKA SMP 2016

“Lebar Sungai”
Andi ingin mengetahui lebar sungai. Di seberang sungai terdapat sebuah pohon. Untuk itu dia menancapkan tongkat sehingga berada pada posisi A, B, C, dan D dengan ukuran seperti pada gambar.
Kesebangunan dan Kekongruenan
Andi ingin mengukur lebar sungai dari tongkat D sampai pohon. Berapa lebar sungai tersebut?
A.     11 m
B.     12 m
C.     15 m
D.     16 m
Pembahasan:
Perhatikan sketsa berikut!
kesebangunan segitiga
Lebar sungai dapat dihitung dengan memanfaatkan kesebangunan segitiga.
Lebar sungai = DP
  \[ \frac{DP}{AP} = \frac{DC}{AB} \]
  \[ \frac{DP}{4 + DP} = \frac{6}{8} \]
  \[ 8DP = 6 \times (4 + DP) \]
  \[ 8DP = 24 + 6DP) \]
  \[ 8DP - 6DP = 24 \]
  \[ 2DP = 24 \]
  \[ DP = \frac{24}{2} = 12 \; m \]
Jadi, lebar sungai = DP = 12 m.
Jawaban: B

Contoh 3: Soal UN Matematika SMP/MTS Tahun 2013

Perhatikan gambar!
Contoh soal un matematika SMP/MTs
Panjang EF adalah ….
A.     20 cm
B.     21 cm
C.     23 cm
D.     26 cm
Pembahasan:
Rumus singkat untuk mencari panjang EF adalah sebagai berikut.
  \[ EF = \frac{AB \times DE + DC \times AE}{DE + AE} \]
  \[ EF = \frac{14 \times 4 + 35 \times 3}{4 + 3} \]
  \[ EF = \frac{56 + 105}{7} \]
  \[ EF = \frac{161}{7} = 23 \; cm \]
Jawaban: C

Contoh 4: Soal UN Matematika SMP/MTS Tahun 2011

Perhatikan gambar berikut!
soal un matematika kesebangunan
Segitiga ABC adalah segitiga siku-siku samakaki. Jika AB = 10 cm dan CD garis bagi sudut C, panjang BD adalah ….
  \[ \textrm{A.} \; \; \; 5 \; cm \]
  \[ \textrm{B.} \; \; \; \left(10 \sqrt{2} − 10 \right) \; cm \]
  \[ \textrm{C.} \; \; \; \left(10 − 5 \sqrt{2} \right) \; cm \]
  \[ \textrm{D.} \; \; \; \left( 5 \sqrt{2} − 5 \right) \; cm \]
Pembahasan:
Perhatikan gambar di bawah!
kesebangunan dan kekongruenan
Berdasarkan gambar, diperoleh informasi bahwa
AB = BC = CE = 10 cm
BD = DE = AE
Mencari nilai AC:
Perhatikan \Delta ABC
Besar sudut BCA adalah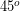 45^{o} (segitiga siku-siku sama kaki), sehingga
  \[ AB : AC = 1 : \sqrt{2} \]
  \[ \frac{AB}{AC} = \frac{1}{\sqrt{2}} \]
  \[ \frac{10}{AC} = \frac{1}{\sqrt{2}} \]
  \[ AC =10 \sqrt{2} \]
Mencari panjang BD:
  \[ BD = AE \]
  \[ BD = AC - CE \]
  \[ BD = \left( 10 \sqrt{2} - 10 \right) \; cm \]
Jawaban: B

Contoh 5: Soal UN Matematika SMP/MTS Tahun 2010

Perhatikan gambar!
kesebangunan dan kekongruenan
P dan Q adalah titik tengah diagonal BD dan AC. Panjang PQ adalah .…
A.     5 cm
B.     4 cm
C.     3 cm
D.     2 cm
Pembahasan:
Rumus cepat untuk mendapatkan panjang PQ adalah
  \[ PQ = \frac{1}{2} \left(DC - AB \right) \]
  \[ PQ = \frac{1}{2} \left(12 - 6 \right) \]
  \[ PQ = \frac{1}{2} \times 6 \]
  \[ PQ = 3 \; cm \]
Jawaban: C

Contoh 6: Soal UN Matematika SMP/MTS Tahun 2007

Segitiga ABC siku-siku di B kongruen dengan segitiga PQR siku-siku di P. Jika panjang BC = 8 cm dan QR = 10 cm, maka luas segitiga PQR adalah ….
A.     24 cm^{2}
B.     40 cm^{2}
C.     48 cm^{2}
D.     80 cm^{2}
Pembahasan:
Perhatikan gambar di bawah!
kekongruenan segitiga
Segitiga ABC dan PQR kongruen, sehingga panjang BC = PQ = 8 cm. Panjang RP dapat diperoleh menggunakan rumus pythagoras.
  \[ PR = \sqrt{QR^{2} - PQ^{2}} \]
  \[ PR = \sqrt{10^{2} - 8^{2}} \]
  \[ PR = \sqrt{100 - 64} \]
  \[ PR = \sqrt{36} \]
  \[ PR = 6 \; cm \]
Mencari luas segitiga PQR:
  \[ L = \frac{a \times t}{2} \]
  \[ L = \frac{ 6 \times 8}{2} \]
  \[ L = \frac{48}{2} = 24 \; cm \]
Jawaban: A
Bagaimana contoh soal dan pembahasan soal UN untuk materi kesebangunan dan kekongruenan untuk level kognitif pengetahuan dan pemahaman. Mudah bukan? Terimakasih sudah mengunjungi atikroest.blogspot.com, semoga bermanfaat!

Komentar

Posting Komentar

Postingan populer dari blog ini

Statistik

Gambar
  Mean, Modus, Median, Jangkauan, Simpangan, dan Ragam 1. Mean Rata-rata hitung dihitung dengan cara membagi jumlah nilai data dengan banyaknya data. Rata-rata hitung bisa juga disebut mean. a) Mean untuk Data Tunggal  b) Mean Untuk Data yang Disajikan Dalam Distribusi Frekuensi   Dengan :  f ᵢ x ᵢ  = frekuensi untuk nilai xi yang bersesuaian xi = data ke-i c) Mean untuk data kelompok                Contoh soal : 1.) Seorang peneliti mencatat banyak bayi yang lahir selama setahun di 20 kecamatan. Hasil pencatatannya disajikan berikut. 136 140 220 193 130 158 242 127 184 213 200 131 111 160 217 281 242 242 281 192  Hitunglah  mean data tersebut! Penyelesaian : 2.) Perhatikan data berikut. nilai ujian 3 4 5 6 7 8 9 frekuensi 3 5 12 17 14 6 3 Seorang siswa dinyatakan lulus jika nilai ujiannya lebih tinggi dari nilai rata-rata dikurangi 1. Dari data di atas, yang lulus adalah : Penyelesaian : Siswa dinyatakan lu...
Baca selengkapnya

Sistem Persamaan Linear

Gambar
Sistem Persamaan Linear Sistem persamaan linear  adalah persamaan-persamaan linear yang dikorelasikan untuk membentuk suatu sistem. Sistem persamaannya bisa terdiri dari satu variabel, dua variabel atau lebih. Dalam bahasan ini, kita hanya membahas sistem persamaan linear dengan dua dan tiga variabel. Sistem Persamaan Linear Dua Variabel (SPLDV) Sistem persamaan linear dua variabel adalah sistem persamaan linear yang terdiri dari dua persamaan dimana masing-masing persamaan memiliki dua variabel. Contoh SPLDV dengan variabel   dan  : dimana  , dan   adalah bilangan-bilangan real. Penyelesaian SPLDV Penyelesaian SP:DV bertujuan untuk menentukan nilai yang memenuhi kedua persamaan yang ada pada SPLDV. Penyelesaian SPLDV terdapat beberapa cara, yaitu: Metode grafik Pada metode grafik ini, langkah-langkah yang dilakukan pertama adalah menentukan grafik garis dari masing-masing persamaan kemudian menentukan titik potong dari kedua g...
Baca selengkapnya