Garis Singgung Lingkaran

By atikroest

Garis singgung lingkaran

Sifat-sifat garis singgung lingkaran

Ada dua sifat yang dimiliki pada garis singgung lingkaran, yakni:

  • Melalui sebuah garis titik di luar lingkaran, dapat dibuat dua buah garis singging.
  • Melalui sebuah titik pada lingkaran, dapat dibuat sebuah garis singgung.

Garis Singgung Persekutuan Luar Dua Lingkaran

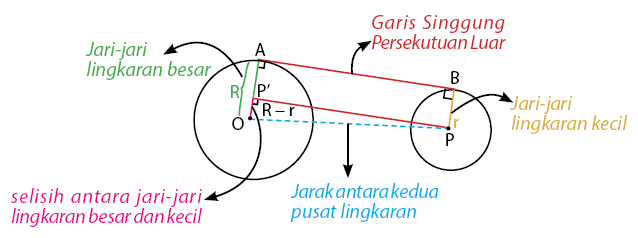
Ulasan materi terkait garis singgung lingkaran yang pertama akan dibahas adalah garis singgung persekutuan luar dua lingkaran. Persamaan garis singgung lingkaran persekutuan luar melibatkan dua lingkaran dan sebuah garis singgung lingkaran. Untuk lebih jelasnya dapat dilihat pada gambar di bawah.

Garis singgung lingkaran
 
Garis AB adalah garis singgung persekutuan luar dua lingkaran. Konsep untuk mengetahui panjang garis singgung persekutuan luar dua lingkaran adalah teorema pythagoras. Langkah pertama adalah proyeksikan titik P ke garis OA. Panjang garis PP’ sama dengan garis AB, sehingga dengan menghitung panjang PP’ maka kita juga akan mendapatkan panjang AB (garis singgung persekutuan dua lingkaran).
Perhatikan bahwa segitiga PP’O merupakan segitiga siku-siku yang siku-siku di P’. Dengan teorema phytagoras dapat diperoleh panjang PP’ yaitu sebagai berikut.
  \[ PP' = \sqrt{OP^{2}-\left( OP'\right)^{2}} \]
Karena OP' = OA - BP = R - r maka,
  \[ PP' = \sqrt{OP^{2} - \left( R - r\right)^{2}} \]
Sehingga, rumus garis singgung persekutuan luar dua llingkaran dapat dinyatakan dalam rumus di bawah.
Rumus mencari panjang garis singgung persekutuan luar dua lingkaran:
  \[ AB = PP' = \sqrt{OP^{2}-(R-r)^{2}} \]
Keterangan:
        AB = PP’ = Garis singgung persekutuan luar lingkaran
        OP = Jarak antara kedua pusat lingkaran
        R = Jari-jari lingkaran besar
        r = jari-jari lingkaran kecil

Garis Singgung Persekutuan Dalam Dua Lingkaran

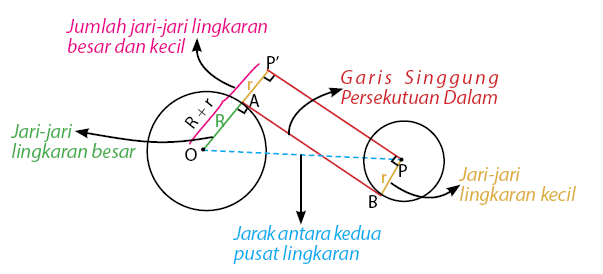
Seperti halnya garis singgung persekutuan luas dua lingkaran, garis singgung persekutuan dalam dua lingkaran juga melibatkan dua buah lingkaran dan sebuah garis singgung. Bedanya terletak pada posisi garis singgung lingkaran. Dua titik singgung lingkaran pada garis singgung persekutuan luar dua lingkaran terletak di sisi yang sama. Sedangkan dua titik singgung lingkaran pada garis singggung persekutuan dalam dua lingkaran terletak bersebrangan. Untuk lebih jelasnya, perhatikan gambar di bawah!

Garis singgung lingkaran
 
Sama halnya dengan garis singgung persekutuan dalam, garis singgung persekutuan luar juga didapat dengan menerapkan konsep teorema phytagoras.
Perhatikan bahwa segitiga PP’O merupakan segitiga siku-siku yang siku-siku di P’. Dengan teorema phytagoras dapat diperoleh panjang PP’ yaitu sebagai berikut.
  \[ PP' = \sqrt{OP^{2}-\left( OP'\right)^{2}} \]
Karena OP' = OA + BP = R + r maka,
  \[ PP' = \sqrt{OP^{2} - \left( R + r\right)^{2}} \]
Sehingga, rumus garis singgung persekutuan dalam dua llingkaran dapat dinyatakan dalam rumus di bawah.
Rumus mencari panjang garis singgung persekutuan dalam
  \[ AB = PP' = \sqrt{OP^{2} - (R + r)^{2}} \]
Keterangan:
        AB = PP’ = Garis singgung persekutuan luar lingkaran
        OP = Jarak antara kedua pusat lingkaran
        R = Jari-jari lingkaran besar
        r = jari-jari lingkaran kecil
 
Begitulah rumus mencari garis singgung lingkaran yang melibatkan dua lingkaran. Selanjutnya, sobat idschool dapat menyimak contoh soal garis singgung persekutuan luar lingkaran dan garis singgung persekutuan dalam lingkaran.

Contoh Soal dan Pembahasan

Contoh Soal Garis Singgung Persekutuan Luar Dua Lingkaran (SOAL UN Matematika SMP 2016)
Dua buah lingkaran memiliki panjang garis singgung persekutuan luar 24 cm dan jarak kedua titik pusat lingkaran 26 cm. Jika panjang jari-jari lingkaran besar 18 cm, maka panjang jari-jari lingkaran yang lain adalah ….
A.     6 cm
B.     8 cm
C.     9 cm
D.     10 cm

Pembahasan:
Berdasarkan data pada soal, kita dapat peroleh gambar di bawah.

garis singgung lingkaran persekutuan luar
 
  \[AB =\sqrt{OP^{2}-\left( R - r\right)^{2}}\]
  \[AB^{2} =OP^{2}-\left( R - r\right)^{2}\]
  \[24^{2} =26^{2}-\left( 18 - r\right)^{2}\]
  \[676 =576 - \left( 18 - r\right)^{2}\]
  \[\left( 18 - r\right)^{2} =676 - 576 \]
  \[\left( 18 - r\right)^{2} = 100 \]
  \[ 18 - r = 10 \]
  \[ - r = 10 -18 \]
  \[ - r = -8 \rightarrow r = 8 \; cm \]
Jadi, panjang jari-jari lingkaran yang lain adalah 8 cm.
Jawaban: D

Contoh Soal Garis Singgung Persekutuan Dalam Dua Lingkaran
Perhatikan gambar berikut!

garis singgung lingkaran dalam

Panjang jari-jari lingkaran besar dan kecil berturut-turut adalah 10 cm dan 5 cm. Jarak kedua pusat lingkaran adalah 25 cm. Panjang garis singgung AB adalah ….
A.     12 cm
B.     15 cm
C.     17 cm
D.     20 cm

Pembahasan:
  \[ AB = \sqrt{OP^{2} - PC^{2}} \]
  \[ AB = \sqrt{OP^{2} - \left( R + r\right)^{2}} \]
  \[ AB = \sqrt{25^{2} - \left( 10 + 5\right)^{2}} \]
  \[ AB = \sqrt{625 - 225} \]
  \[ AB = \sqrt{400} \]
  \[ AB = 20 \; cm \]
Jadi, panjang garis singgung AB adalah 20 cm.
Jawaban: D
 
Segi Empat Tali Busur

Segi Empat Tali Busur: Pengertian, Sudut, dan Sifat-sifatnya


Segi empat tali busur adalah salah satu materi yang dipelajari pada mata pelajaran matematika. Segi empat tali busur sendiri memiliki sebutan lain, yakni segi empat siklik.

Segi empat tali busur identik dengan bangun datar lingkaran. Mengapa demikian? Hal tersebut disebabkan oleh posisi segi empat tali busur yang terletak dalam lingkaran.

Tali busur sendiri merupakan salah satu unsur yang ada dalam bangun datar dalam lingkaran. Melalui tali busur, segi empat pun akan terbentuk di dalam suatu lingkaran.

Untuk memahami segi empat tali busur lebih dalam, simak beberapa penjelasan mengenai segi empat tersebut pada di bawah ini.

Pengertian Segi Empat Tali Busur

Dikutip dari buku Matematika untuk SMP dan MTs Kelas VIII yang ditulis oleh Budi Suryatin, dkk, segi empat tali busur adalah segi empat yang titik-titik sudutnya terletak pada suatu lingkaran.

Menurut Budi Suryatin, dkk, sisi-sisi pada segi empat tali busur merupakan tali busur lingkaran. Tali busur adalah garis lurus yang menghubungkan dua titik pada keliling lingkaran.

Berbeda dengan diameter, tali busur tidak melalui titik pusat lingkaran. Terbentuknya empat tali busur di dalam suatu lingkaran disebut sebagai segi empat tali busur.

Untuk lebih jelasnya, perhatikan gambar berikut ini.


Pada gambar tersebut, titik O adalah titik pusat lingkaran dan titik A, B, C, serta D adalah titik yang terletak pada keliling lingkaran tersebut.

Ruas garis AB, BC, CD, dan DA adalah tali-tali busur lingkaran. Tali-tali busur tersebut membentuk segi empat ABCD, dan selanjutnya disebut segi empat tali busur.

Sudut dalam Segi Empat Tali Busur

Jumlah sudut yang saling berhadapan pada segi empat tali busur adalah 180°

Untuk lebih memahami posisi sudut dalam segi empat tali busur, perhatikan gambar di bawah ini.


Berdasarkan pada gambar di atas, maka jumlah sudut yang saling berhadapan pada segi empat tali busur:

  • ∠ABC + ∠ADC = 180°

  • ∠BAD + ∠ BCD = 180°

Sifat-Sifat Segi Empat Tali Busur

Sifat-sifat segi empat tali busur adalah sifat yang dimiliki oleh persegi dalam lingkaran yang menjadi karakteristik dari bangun tersebut.

Segi empat tali busur mempunyai beberapa sifat. Sifat-sifat tersebut adalah sebagai berikut:

  • Jumlah dua sudut yang saling berhadapan pada segi empat tali busur adalah 180°

  • Segi empat tali busur yang salah satu diagonalnya merupakan diameter lingkaran disebut segi empat tali busur siku-siku.

  • Segi empat tali busur yang kedua diagonalnya merupakan diameter lingkaran akan membentuk bangun persegi panjang.

Sekian pembahasan mengenai garis singgung lingkaran yang memuat rumus garis singgung lingkaran persekutuan dalam dan garis singgung lingkaran persekutuan luar. Terimakasih sudah mengunjungi atikroest.blogspot.com, semoga bermanfaat..

Komentar

Posting Komentar

Postingan populer dari blog ini

Kesebangunan dan Kekongruenan (soal dan pembahasan)

Gambar
Kesebangunan dan Kekongruenan Hallo sobat atikroest, pada halaman ini akan mengupas tentang contoh soal kesebangunan dan kekongruenan. Seperti kisi-kisi yang telah dikeluarkan BSNP, materi kesebangunan dan kekongruenan akan kembali muncul di ujian nasional. Kisi-kisi untuk kesebangunan dan kekongruenan diberikan dalam 3 (tiga) level kognitif, yaitu pengetahuan dan pemahaman, aplikasi, dan penalaran. Halaman ini akan membahas kisi-kisi UN 2019 dengan materi kesebangunan dan kekongruenan untuk level pengetahuan dan pemahaman. Simak kumpulan soal UN dengan materi kesebangunan dan kekongruenan pada pembahasan di bawah. BAGIAN I Contoh 1: Soal UN Matematika SMP/MTS Tahun 2014 Perhatikan gambar! Banyak pasangan segitiga yang kongruen adalah …. A.     1 B.     2 C.     3 D.     4 Pembahasan: Banyak pasangan segitiga yang kongruen ada 2 pasang, yaitu         Jawaban: B Contoh 2: Soal UN Matematika SMP/MTS...
Baca selengkapnya

Trigonometri

Gambar
Fungsi Trigonometri dan Sudut Istimewa pada Trigonometri By atikroest Halo, squad...! Selamat datang kembali di official page nya atikroest.blogspot.com. Tempat di mana squad dapat belajar kapan saja, dan di mana saja. Kali ini, akan membahas mengenai fungsi trigonometri dan sudut istimewa pada trigonometri. Trigonometri adalah cabang ilmu matematika yang mempelajari sudut dalam segitiga dan fungsi trigonometri. Perbandingan trigonometri terdiri atas fungsi sinus, cosinus, tangen, dan fungsi kebalikan dari ketiga fungsi tersebut. Definisi Sudut dan Ukuran Sudut Sudut adalah suatu bangun yang dibentuk oleh suatu titik pangkal tertentu dan dua sinar dengan titik pangkal yang sama. Tempat titik pangkal yang merupakan pertemuan dua sinar disebut  titik sudut . Sedangkan dua sinar tersebut dinamakan  kaki sudut . Untuk lebih jelasnya perhatikan gambar berikut. Perbandingan Trigonometri Perbandingan trigonometri meliputi fungsi sinus, cosinus, tangen...
Baca selengkapnya

Bangun datar

Gambar
Ciri-ciri dan Sifat Bangun Datar   Bangun datar adalah suatu bentuk dua dimensi dari bangun-bangun yang mempunyai permukaan datar pada luas, panjang, lebar, dan kelilingnya. Macam-macam bangun datar, antara lain persegi, persegi panjang, lingkaran, segitiga, jajar genjang, belah ketupat, layang-layang, trapesium, segi lima atau pentagon, dan segi enam atau hexagon. Kamu juga bisa membaca salah satu rekomendasi buku berikut ini jika ingin mengetahui lebih luas lagi tentang bangun datar yang belum kamu ketahui. Berikut ini adalah beberapa ciri-ciri dan sifat bangun datar, antara lain sebagai berikut: 1. Persegi Persegi adalah bangun datar dua dimensi yang memiliki bentuk pada keempat rusuk yang sisinya sama panjang dan memiliki empat sudut siku-siku sebesar 90 derajat. Perhatikan contoh gambar di bawah ini. Ciri-ciri dan sifat bangun datar persegi, antara lain: Memiliki sisi-sisi yang sama panjang. Memiliki dua diagonal yang sama panjang (keduanya saling berpotongan dan membentuk teg...
Baca selengkapnya